Statistische Abhängigkeit über Baumdiagramm
Bestimmung
© 2016
- 2025
Basiswissen|
Einordnung|
Grundidee|
Mützenmännchen|
Baumdiagramm|
Überprüfung allgemein|
Überprüfung Mützenmännchen|
Schluss
Basiswissen
Hat man ein Baumdiagramm mit relativen Häufigkeiten zu zwei Merkmalen, dann kann man leicht erkennen, ob die zwei Merkmale voneinander statistisch unabhängig sind: ganz unten im Baumdiagramm gibt es von links nach rechts gehend vier Zahlen an den Ausgängen, die sogenannten Ausgangswahrscheinlichkeiten. Wenn die 1. und die 3. Ausgangswahrscheinlichkeit gleich sind und gleichzeitig auch die 2. und die 4. Ausgangswahrscheinlichkeit gleich sind, dann sind die zwei betrachteten Merkmale zueinander unabhängig. Das ist hier ausführlich erklärt.
Einordnung
- Es geht hier um die statistische Abhängigkeit von zwei Merkmalen.
- Es soll überprüft werden: sind abhängig oder nicht.
- Es gibt verschiedene Methoden, wie man das macht.
- Eine Möglichkeit ist eine 👉 Vierfeldertafel
- Eine andere das Baumdigramm.
- Hier geht es um das 👉 Baumdiagramm
Grundidee
- Hat man ein Baumdiagramm mit relativen Häufigkeiten, ...
- dann kann man leicht die statistische Abhängigkeit überprüfen.
- Das wird hier an einem Beispiel erklärt.
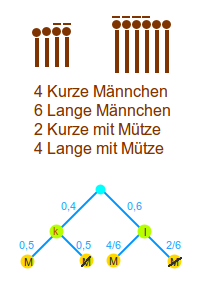
Mützenmännchen
- Zeichne vier kurze Strichmännchen.
- Zeichne sechs lange Strichmännchen.
- Setze zwei der kurzen Strichmännchen eine Mütze auf.
- Setze vier der langen Strichmännchen eine Mütze auf.
Baumdiagramm
- Wir zeichnen ein senkrecht stehendes Baumdiagramm.
- Fange oben an mit zwei Ästen.
- Schreibe an den linken Ast unten: k (für "kurz").
- Schreibe an den rechten Ast unten: l (für "lang").
- Schreibe als Wahrscheinlichkeit an den linken Ast: 0,4
- Schreibe als Wahrscheinlichkeit an den rechten Ast: 0,6
- Zeichne vom linken Ast aus zwei weitere Äste nach unten.
- Schreibe an den linken Ast unten: M ("Mütze").
- Schreibe an den rechten Ast unten: durchgestrichenes M (keine Mütze)
- Schreibe als Wahrscheinlichkeit am linken Ast: 0,5
- Schreibe als Wahrscheinlichkeit am rechten Ast: 0,5
- Zeichne vom rechten oberen Ast aus zwei neue Äste nach unten.
- Schreibe an den linken Ast unten: M
- Schreibe an den rechten Ast unten: M durchgetrichen
- Schreibe als Wahrscheinlichkeit an den linken Ast: 4/6 oder 2/3
- Scheibe als Wahrscheinlichkeit an den rechten Ast: 2/6 oder 1/3
- Siehe allgemein auch 👉 Baumdiagramm
Überprüfung allgemein
- Man muss nur die vier unteren Äste betrachten.
- Dort sieht man nur nach den vier Wahrscheinlichkeiten, falls ...
- Erste Bedingung: 1. Zahl gleich 3. Zahl und ...
- Zweite Bedingung: 2. Zahl gleich 4. Zahl, dann sind ...
- die zwei Merkmale unabhängig.
- Ansonsten: abhängig.
Überprüfung Mützenmännchen
- Erste Bedingung: 0,5 = 2/3 gilt nicht
- Zweie Bedingung: 0,5 = 1/3 gilt nicht
Schluss
- Es gehen nicht alle Bedingungen auf (sogar gar keine).
- Das heißt: die zwei Merkmale sind statistisch abhängig:
- Länge Männchen sind eher Mützenträger als kurze Männchen.