Lösungsformel
Abstand heißt hier: die kürzeste Entfernung. Kurz vorgestellt wird eine Berechnungsmethode mit Hilfe von Vektoren und Geraden (analytische Geometrie). => Ganzen Artikel lesen …
Abstand
Definition
Der kürzeste Weg zwischen zwei Dingen heißt Abstand. Man kann den Abstand angegeben in zum Beispiel Zentimetern, Metern oder Kilometern. Hier stehen Beispiele dazu. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
Mathematik
Dezimalpunkt, Tausendertrennpunkt und Multiplikations-Punkt: diese drei wichtigen Bedeutungen sind hier kurz erklärt. Viele weitere Bedeutungen stehen unter => Punkte
Geschlossen, hin die Richtung von etwas
Wenn ein Geschäft geschlossen ist, dann ist es zu. Auch ein verschlossenes Gefäß kann zu sein. Die Wendung zu spät heißt, dass man später als es gut gewesen wäre ist. => Ganzen Artikel lesen …
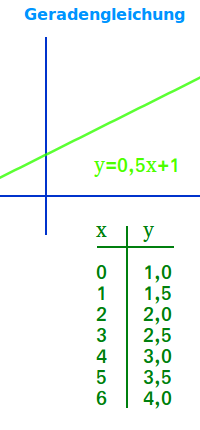Gerade
Übersicht
Eine Gerade in der Mathematik ist eine Linie ohne Ecken, Lücken, Kurven oder Enden: sie ist unendlich lang gedacht. Die kürzeste Verbindung zwischen zwei Punkten liegt immer auf einer Geraden. Hier werden Geraden in verschiedenen Teilgebieten der Mathematik kurz vorgestellt. => Ganzen Artikel lesen …
Anleitungen
Ein Punkt P und eine Ebene E sind gegeben. Der Abstand des Punktes zur Ebene ist die Länge der kürzesten Strecke vom Punkt zur Ebene. Hier stehen Berechnungsformeln. => Ganzen Artikel lesen …
Lösungsweg
Zwei zueinander parallele und nicht identische Geraden haben überall denselben Abstand zueinander. Sind die zwei Geraden nicht parallel zueinander dann nennt man sie windschief. Für zwei windschiefe Geraden gibt es immer genau einen kürzesten Abstand. Hier steht eine stark verkürzte Anleitung für die Berechnung dieses Abstandes. => Ganzen Artikel lesen …
Formeln
Der Abstand zwischen zwei Punkten meint die kürzestmögliche Strecke zwischen diesen zwei Punkten. Man kann den Abstand berechnen für zwei Punkte in einer Ebene (2D), im Raum (3D) oder auch auf einer Kugeloberfläche. Diese Fälle sind hier kurz erklärt. => Ganzen Artikel lesen …
Kurzanleitung
Man hat zwei Punkte in einem xyz-Koordinatensyste, kann man den Abstand leicht berechnen: man bildet einen Verbindungsvektor vom einen zum anderen Punkt. Von diesem Punkt berechnet man dann die Vektorlänge. Siehe auch => Abstand von Punkt zu Punkt
