Vektor aus zwei Punkten
Berechnung
© 2016
- 2025
Basiswissen
Man hat zwei Punkte in einem xyz-Koordinatensystem gegeben. Gesucht ist ein Vektor, der vom ersten zum zweiten Punkt führt. Beispiel: der Vektor vom Punkt (8|5|3) zum Punkt (10|9|4) hätte die Vektorkoordinaten (2|4|1). Den Ergebnisvektor nennt man auch Verbindungs- oder Verschiebungsvektor. Das ist hier kurz erklärt.
Kurz-Anleitung
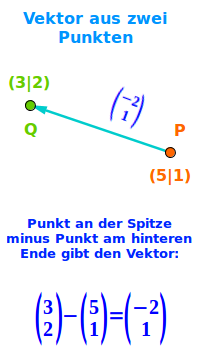
- Man hat zwei 3D-Punkte in einem 3D-Koordinatensystem.
- Man will einen Vektor zwischen den beiden Punkten berechnen.
- Ein Vektor hat einen Anfang (ohne Spitze) und ein Ende (mit Spitze).
- Zuerst entscheidet man bei welchem Punkt die Pfeilspitze sein soll.
- Dann rechnet man: Punkt der Spitze minus anderen Punkt.
- Siehe auch 👉 Vektor minus Vektor [Spitze minus Anfang]
Beispiel zur Berechnung
- Man hat die Punkte: P(3|2|1) und Q(8|6|4)
- Man will den Vektor von P nach Q berechnen.
- Die Spitze soll also bei Q sein.
- Man rechten immer: Spitze minus Anfang
- Also rechnet man: Q-P, das gibt: (5|4|3).
- Als Vektor schreibt man das übereinander.
- Das ist der Vektor von P nach Q.
- Siehe auch 👉 Vektor
Wie benennt man den Ergebnisvektor?
Der berechnete Vektor ist rein mathematisch ein Differenzvektor, da er als Ergebnis einer Minusrechnung (Differenz) enstanden ist. Anschaulich gedeutet, kann man mit diesem Differenzvektor den einen Punkt hin zum anderen Punkt schieben. Oder alternativ kann man auch vom ersten zum zweiten Punkt gehen, wenn man den Vektor im ersten Punkt anfangen lässt. So gedeutet ist der Differenzvektor auch ein Verbindungsvektor oder ein 👉 Verschiebungsvektor