Basiswissen

Wofür gibt es Steigungsdreiecke?

• Steigungsdreiecke gehören immer zu Graphen von Funktionen.
  

• Eine Gerade in einem Koordinatensystem nennt man zum Beispiel Graph.
  

• Auch Parabeln oder Hyperbeln in Koordinatensystemen nennt man Graph.
  

• Graphen gehören oft zu Gleichungen, oft von Funktionen.
  

• Für jeden Graphen kann man Steigungsdreiecke zeichnen.
  

Wozu sind Steigungsdreieck gut?

• Mit einem Steigungsdreieck kann man leicht die Steigung eines Graphen ausrechnen.
  

• Man recht einfach: Höhe des Steigungsdreiecks geteilt durch die Breite.
  

• Das Ergebnis ist dann die Steigung des Graphen.
  

• Mehr unter Steigung aus Steigungdreieck (externer Link)
  

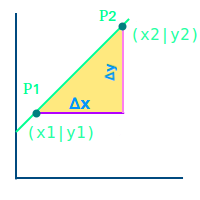
Was ist ein Steigungsdreieck?

• Ein Dreieck, dessen längste Seite durch zwei Punkt auf dem Graphen geht.
  

• (Welche Punkte von dem Graphen man dafür nimmt, ist egal.)
  

• Den linken Punkt nennt man oft P1 mit den Koordinaten (X1|Y1).
  

• Den rechten Punkt nennt man oft P2 mit den Koordinaten (X2|Y2).
  

• Eine der kürzeren Seiten von dem Dreieck verläuft waagrecht (parallel zur x-Achse).
  

• Die andere der zwei kürzen Seiten verläuft senkrecht (parallel zur y-Achse).
  

• Siehe auch Steigungsdreieck zeichnen ↗
  

Welche Fachworte gibt es?

• Die Länge der waagrechten Seite heißt ∆Y, mehr unter Delta x ↗
  

• Die Länge der senkrechten Seie heißt ∆X, mehr unter Delta y ↗