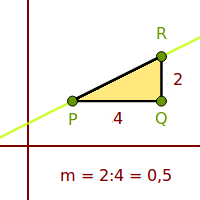
Steigungsdreieck aus Graph
Anleitung
© 2016
- 2025
Basiswissen|
Vorab|
Längste Seite|
Waagrechte Seite|
Senkrechte Seite|
Fertiges Dreieck|
Beschriften|
Steigung|
Tipps
Basiswissen
Man hat den Graphen einer Funktion, zum Beispiel einer Geraden oder einer Parabel. Für den Graphen soll ein Steigungsdreieck gezeichnet werden. Das ist hier ausführlich erklärt.
Vorab
- Angenommen man hat den Graphen einer Funktion schon gegeben.
- Der Graph kann eine Gerade sein oder auch eine Parabel oder sonstetwas.
- Die Form des Graphen ist eigentlich egal, am Anfang geht es aber meistens um Geraden.
- Das Steigungsdreieck hat drei Seiten: eine längste, eine waagrechte und eine senkrechte.
- Jetzt wird erklärt, wie man diese drei Seiten zeichnet:
Längste Seite
- Man markiert irgendwelche zwei Punkte (verschiedenen) Punkte direkt auf dem Graphen.
- Den linken Punkt nennt man oft P und den rechten Punkt zum Beispiel R.
- Gut zu zeichnen ist es, wenn diese Punkte 4 bis 10 cm auseinanderliegen.
- Man verbindet diese zwei Punkte mit einem Lineal (vielleicht farbig).
- Bei einer Geraden liegt diese Linie direkt auf der Geraden.
- Das ist die längste Seite des Steigungsdreiecks.
Waagrechte Seite
- Man geht zum linken der zwei Punkte, also zu P.
- Man zeichnet eine dünne waagrechte Hilfslinie durch diesen Punkt.
- Waagrecht meint von links nach rechts, also parallel zur x-Achse.
- Man zeichnet die Linie mindestens so lang, dass sie so weit nach rechts geht, ...
- wie der rechte der zwei Punkte liegt.
Senkrechte Seite
- Man geht zum rechten der zwei Punkte, also zu R.
- Man zeichnet eine dünne senkrechte Linie durch diesen Punkt.
- Man zeichnet diese Linie so lang, dass sie die waagrechte Hilfslinie schneidet.
- Man markiert den Schnittpunkt.
- Der Schnittpunkt heißt hier Q.
Fertiges Dreieck
- Jetzt hat man die drei Ecken des Steigungsdreiecks:
- Man verbindet P, Q und R zu einem gut sichtbaren Dreieck.
- Das ist das Steigungsdreieck.
Beschriften
- Oft beschriftet man noch die beiden kürzeren Seiten.
- Man schreibt dazu an die waagrechte Seite, wie lang sie ist.
- Man schreibt auch an die senkrechte Seite, wie lang sie ist.
Steigung
- Man könnte jetzt auch noch die Steigung m berechnen.
- Man rechnet: Länge der senkrechten Seite geteilt durch die Länge der waagrechten Seite.
- Das Ergebnis ist die Steigung. Sie wird oft mit einem kleinen m abgekürzt.
- Wenn die längers Seite des Dreiecks von links nach rechts bergab geht, muss noch ein Minuszeichen vor die Steigung.
- Man kann diese Steigung jetzt noch an oder in das Steigungsdreieck schreiben.
- Man schreibt zum Beispiel: Steigung m = 1,5 oder m = -1
- Siehe auch 👉 Steigung aus Steigungsdreieck
Tipps
- Eine Gerade hat immer diesselbe Steigung, egal, wie wo P und R liegen.
- Aber: P und R müssen an verschiedenen Stellen auf dem Graphen liegen.
- Eine Parabel oder Hyperbel kann viele verschiedene Steigungen haben.
- Hier erhält man für unterschiedliche Punkte P und R auch unterschiedliche Steigungen.
- Siehe auch 👉 Steigungen