Spurpunkte von Ebenen berechnen
Anleitung
© 2016
- 2025
Basiswissen|
Den einfachsten Weg wählen|
In Achsenabschnittsform|
In Koordinatenform|
In Parameterform
Basiswissen
Die beste Art der Berechnung hängt davon ab, in welcher Form die Ebenengleichung E gegeben ist. Die Spurpunkte sind die Schnittpunkte einer gegebenen Ebene mit den drei Ebenen des Koordinatensystems. Es werden hier drei verschiedene Varianten - für jeweils dieselbe Ebene - kurz erklärt.
Den einfachsten Weg wählen
- a) sehr einfach: E ist gegeben in der 👉 Achsenabschnittsform der Ebene
- b) einfach: E ist gegeben in der 👉 Koordinatenform der Ebene
- c) Aufwändig: E ist gegeben in der 👉 Parameterform der Ebene
- Für den Fall c: Form eventuell erst umwandeln
In Achsenabschnittsform
- Sehr einfach:
- E: x/2 + y/4 + z/2 = 1
- Die Nenner der drei Variablen geben direkt die Achsenabschnitte:
- S1: die x-Achse wird geschnitten bei x=2
- S2: die y-Achse wird geschnitten bei y=4
- S3: die z-Achse wird geschnitten bei z=2
- Damit ergeben sich die Spurpunkte:
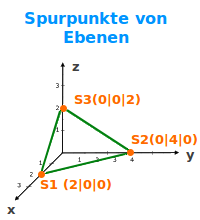
- S1 (2|0|0) ✔
- S2 (0|4|0) ✔
- S3 (0|0|2) ✔
In Koordinatenform
- Einfach:
- E: 2x + 1y + 2z = 4
- S1: Spurpunkt liegt auf der x-Achse, also: y=0 und z=0
- S2: Spurpunkt liegt auf der y-Achse, also: x=0 und z=0
- S3: Spurpunkt liegt auf der z-Achse, also: x=0 und y=0
- Damit ergeben sich die drei Spurpunkte:
- S1: Einsetzen: E: 2x + 1·0 + 2·0 = 4 ⇔ x=2, also: S1 (2|0|0) ✔
- S2: Einsetzen: E: 2·0 + 1·y + 2·0 = 4 ⇔ y=4, also: S2 (0|4|0) ✔
- S3: Einsetzen: E: 2·0 + 1·0 + 2·z = 4 ⇔ z=2, also: S2 (0|0|2) ✔
In Parameterform
- Aufwändig:
- E: x = (0|2|1) + r(2|-2|-1) + s(0|2|-1)
- S1, Schnittpunkt mit der x-Achse gilt: y=0 und z=0
- S2, Schnittpunkt mit der y-Achse gilt: x=0 und z=0
- S3, Schnittpunkt mit der z-Achse gilt: x=0 und y=0
- Spurpunktpunktbedingunen für S1, S2 und S2 formulieren:
- Für S1 gilt: x = 0 + 2r + 0s
- Für S1 gilt: 0 = 2 - 2r + 2s I
- Für S1 gilt: 0 = 1 - 1r - 1s II
- Für S2 gilt: y = 2 - 2r + 2s
- Für S2 gilt: 0 = 0 + 2r + 0s I
- Für S2 gilt: 0 = 1 - 1r - 1s II
- Für S3 gilt: z = 1 - 1r - 1s
- Für S3 gilt: 0 = 0 + 2r + 0s I
- Für S3 gilt: 0 = 2 - 2r + 2s II
- Für S1, S2 und S3 jeweils die Gleichungssysteme I und II lösen
- Für S1: r=1 und s=0
- Für S2: r=0 und s=1
- Für S3: r=0 und s=-1
- Für S1, S2 und S2 die r- und s-Werte in jeweils erste Gleichung einsetzen:
- Für S1: x = 0 + 2·1 + 0·0 ⇔ x = 2
- Für S2: y = 2 - 2·0 + 2·1 ⇔ y = 4
- Für S3: z = 1 - 2·0 - 1·(-1) ⇔ z=2
- S1 (2|0|0) ✔
- S2 (0|4|0) ✔
- S3 (0|0|2) ✔