Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

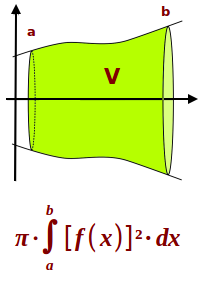
Rotationskörpervolumen berechnen

V = π·∫[f(x)]²·dx

© 2016 - 2025

Basiswissen · Formel · Legende · Rechenbeispiel

Basiswissen

Lässt man die Kurve (Graphen) einer Funktion f(x) einmal um die x-Achse kreisen (rotieren), dann entsteht durch diese Bewegung die Hülle eines Körper. Das Volumen des Körper kann mit Hilfe der Funktionsgleichung f(x) berechnet werden. Das ist hier kurz erklärt.

Bildbeschreibung und Urheberrecht — Der Graph verläuft oberhalb der x-Achse, er wird gedanklich um die x-Achse gedreht, wodurch ein 3D-Körper entsteht. Kennt man die Funktionsgleichung, kann man dieser das Volumen des Körpers berechnet werden.☛

Formel

V = π·∫[f(x)]²·dx

Legende

V = Volumen des Rotationskörper[s]

π = Etwa 3,14, die Kreiszahl ↗

∫ = das Integralzeichen ↗

· = ein übliches Malzeichen ↗

² = Quadrierung oder hoch zwei ↗

dx = ein Differential ↗

Rechenbeispiel

Man hat zum Beispiel die Funktion: f(x) = 3x

Das Volumen des Rotationskörpers von x=1 bis x=2 soll berechnet werden.

1. Schritt: [f(x)]² - also den Funktionsterm hoch zwei rechnen, das gibt hier: 9x²

2. Schritt: diesen quadrierten Term aufleiten (Stammfunktion bilden), hier: ⅓·9·x³ = 3x³

3. Rechte Integrationsgrenze eingesetzt minus linke Integrationsgrenze eingesetzt: 3·3³-3·1³ = 80

4. Ergebnis notieren: das Volumen von Zwischen den x-Werten 1 und 3 beträgt: 80 Volumeneinheiten. ✔