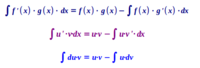Partiell integrieren
Regel | Beispiele
Basiswissen
Partiell integrieren, auch Produktintegration genannt, ist ein Ansatz, um Stammfunktionen zu finden, wenn der Funktionsterm das x auf zwei Seiten eines Malzeichens stehen hat. Der Ansatz über die partielle Integration führt oft - aber nicht immer zuverlässig - zum Ziel. Es gibt aber Tipps, die Erfolgswahrscheinlichkeit zu erhöhen. Das ist hier kurz vorgestellt.
Wann ist das Verfahren sinnvoll?
- a) Der Funktionsterm ist ein Produkt.
- b) Der eine Faktor wird beim ableiten einfacher.
- c) Der andere Faktor wird beim aufleiten nicht schwieriger.
Formeln zum partiellen Integrieren
- Integral von [f'(x)·g(x)] = f(x)·g(x) - Integral von [f(x)·g'(x)]
- Integral von [du·v] = u·v - Integral von [u·dv]
- Integral von [u'·v] = u·v - Integral von [u·v']
Legende
- Die drei Formeln sind identisch und führen immer zum selben Ergebnis.
- g(x) und u meinen dasselbe.
- f(x) und v meinen dasselbe.
- g'(x) und du meinen dasselbe.
- f'(x) und dv meinen dasselbe.
- u' ist wie g'(x)
- v' ist wie f'(x)
- du ist wie u'.
- dv ist wie v'.
Erläuterung
- Mit Hilfe der Formel kann man eine Stammfunktion finden bzw. aufleiten.
- Die eigentliche Funktion ist dabei als Produkt geschrieben.
- Produkt meint: der Funktionsterm hat ein Malzeichen.
- Anders gesagt: der Integrand steht in Produktform.
- g(x) bzw. u ist der Faktor links vom Malzeichen.
- f'(x) bzw. dv ist der Faktor rechts vom Malzeichen.
Allgemeine Anleitung, Schritt für Schritt
- 1) Man betrachtet sich den Integranden.
- 1) Der Integrand muss ein Produkt sein (Malterm).
- 1) Das x steht einmal links vom Malpunkt, und einmal rechts vom Malpunkt.
- 1) Was links vom Malpunkt steht heißt linker Faktor.
- 1) Was rechts vom Malpunkt steht heißt rechter Faktor.
- 2) Man entscheidet jetzt, wer u' und wer v ist.
- 2) Was aufgeleitet als Term nicht schwieriger wird u'[2].
- 2) Was abgeleitet als Term einfacher wird, wird v[3].
- 3) Man weiß jetzt, was u' und was v sind.
- 3) Man schreibt einen Vierblock hin und berechnet die fehlenden Terme:
- 3) u = …
- 3) u' = …
- 3) v = …
- 3) v' = …
- 4) Man setzt die Zwischenergebnisse des Viererblocks ein:
- 4) Integral von [u'·v] = u·v - Integral von [u·v']
- 5) Man berechnet das noch vorhandene Integral von [u·v']
Beispielrechnung
- Man hat die den Funktionsterm x²·x.
- Gesucht ist die Stammfunktion ∫x²·x·dx
- Der Integrand ist das x²·x, das soll aufgeleitet werden.
- Links vom Malpunkt steht das x². Das ist das g(x) bzw. u.
- Rechts vom Malpunkt steht das x. Das ist das f'(x) bzw. dv.
- Man schreibt u, du, v und dv als "Viererblock":
- u = x²
- u' oder du = 2x (man leitet u dazu ab.)
- v = 0,5·x² (man leitet dv dazu auf.)
- v' oder dv = x
- Jetzt u, du (u'), v und dv (v') in die Formel einsetzen:
- x²·0,5·x² - ∫0,5·x²·2x·dx
- Integral ausrechnen gibt:
- x²·0,5·x² - 0,25·x^4
- Zusammenfassen gibt:
- 0,25·x^4 ✔
Klappt das immer?
- Nein, das Verfahren führt nicht immer zum Erfolg.
- Es ist intelligentes Probieren ohne Erfolgsgarantie.
Die Faktor-1-Methode
- Wende die Faktor-1-Methode an: hat man eine Funktion, die leicht abzuleiten ist, schreibe sie mit 1· davor, z. B. kann man ln(x) schreiben als 1·ln(x).
Standardbeispiel
- Integriere x·e^x·dx
- Man wählt x als g(x)
- f(x) = e^x
- g(x) = x
- f'(x) = e^x
- g'(x) = 1
- Anwendung der Formel von oben gibt:
- Integral x·e^xdx = x·e^x - Integral von [(e^x)·1]dx
- Vereinfachen gibt: xe^x - e^x = (x-1)e^x
Standardaufgaben
- x·cos(x)dx gibt x·sin(x)-cos(x)
- x·sin(x)dx gibt -x·cos(x)+sin(x)
- sin(x)·cos(x)dx gibt -0,5·[cos(x)]²
- 1·ln(x)dx gibt x·ln(x)-x
- e^x·(2-x²)dx gibt e^x·(2x-x²)
- x²·e^(-x)dx gibt (-x²-2x-2)·e^(-x)
- e^x·sin(x)dx gibt 0,5e^x·[sin(x)-cos(x)]
- x·ln(x)dx gibt 0,5·x²·ln(x)-0,25·x²
Syonyme
Fußnoten
- [1] Mit u und v: Partielle Integration. In: Spektrum Lexikon der Physik. Online: https://www.spektrum.de/lexikon/mathematik/partielle-integration/9431
- [2] Typische Terme, die beim Aufleiten nicht schwerer werden sind e^x oder generell die Terme von e-Funktionen sowie sin(x) oder cos(x).
- [3] Typische Terme, die beim Ableiten einfacher werden können sind ganzrationale Funktionsterme (x², 4x etc.) sowie Umkehrfunktionen wie ln(x) oder arcsin(x).
