ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Nabla-Operator

∇

© 2016 - 2025


Basiswissen · Der Nabla-Operator zur Berechnung des Gradienten eines Skalarfeldes · Der Nabla-Operator zur Berechnung der Rotation eines Vektorfeldes


Basiswissen


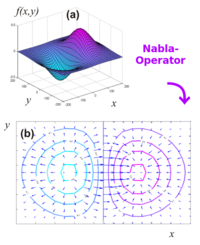
Mit Hilfe des Nabla-Operators wandelt man zum Beispiel ein Skalarfeld (nur Zahlen) in ein Vektorfeld um: die Vektoren zeigen an, in welche Richtung sich die Zahlenwerte am stärksten ändern.



Bildbeschreibung und Urheberrecht
Der Graph oben zeigt für jede xy-Position eine Höhe z als Skalar (Zahl) an, die Visualisierung ergibt eine geschwungene Fläche. Der Nabla-Operator erzeugt daraus ein Vektorfeld b: jeder Vektor gibt die Richtung und Stärke der Steigung der Fläche aus a an. © Christophe Finot ☛


Der Nabla-Operator zur Berechnung des Gradienten eines Skalarfeldes


  • Der Vektor wird als Gradient bezeichnet.


Dieses Bild ist für das Verständnis des Textes nicht wichtig. Das Bild wird im Text nicht erwähnt.
Der Gradient eines Skalarfeldes entsteht dadurch, dass man alle partiellen Ableitung rechnerisch in einem anschaulich deutbaren Vektor, dem Gradienten zusammenfasst.

  • Der Gradient gibt an, wie stark sich ein Skalarfeld an einer Stelle ändert.
  • Er zeigt in die Richtung der größten Änderung.

Über den Nabla-Operator kann man dann jedem Punkt eines Skarfeldes einen Vektor zuordnen. Das hat zur Folge dass man letztendlich ein Vektorfeld hat. Die einzelnen Vektoren gegeben dann an, wie stark und in welche Richtung sich die Skalaren Werte ändern.


Dieses Bild ist für das Verständnis des Textes nicht wichtig. Das Bild wird im Text nicht erwähnt.
Das Bild zeigt, wie aus einen gegebenen Skarlarfeld über den Nabla-Operator ein geometrisch sinnvoll zu deutendes Vektorfeld wird.

Das über den Nabla-Operator entstandene Vektorfeld lässt sich nun geometrisch sinnvoll deuten. Das ist näher erläutert im Artikel Gradient eines Skalarfeldes ↗

Der Nabla-Operator zur Berechnung der Rotation eines Vektorfeldes


  • Die Rotation ist anschaulich gedeutet die Drehung eines kleines Probekörpers um sich selbst.
  • Mit Hilfe des Nabla Operators kann jedem Punkt im Raum die sogenannte Rotation zugeordnet werden.