Basiswissen

Was ist der Kerngedanke?

• Man geht auf einen beliebigen Punkt von f(x).
  

• Die Steigung von diesem Punkt ist gleich dem y-Wert von f'(x):
  

• Anders gesagt: Der Funktionswert von f'(x) ist die Steigung von f(x).
  

• Beispiel: wo f(x) waagrecht verläuft ist die Steigung von f(x) Null.
  

• Also hat dort f'(x) den y-Wert 0.
  

Was man vorab wissen sollte

• Die Steigung von f(x) ist dort positiv, wo ...
  

• der Graph von links nach rechts betrachtet bergbauf geht.
  

• Die Steigung von f(x) ist dort negativ, wo ...
  

• der Graph von links nach rechts betrachtet bergab geht.
  

• Die Steigung von f(x) ist dort gleich null,
  

• der Graph einen Hoch- Tief- oder Sattelpunkt hat.
  

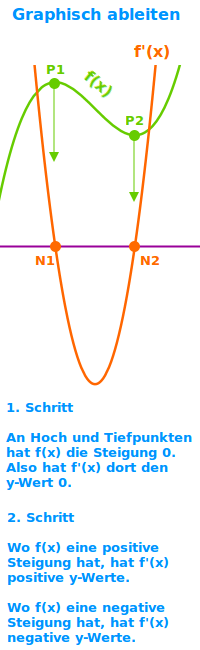
1. Schritt: charakteristische Punkte auswerten

• Man fängt immer mit charakteristischen Punkten an:
  

• f(x) hat Extrempunkt ⭢ f'(x) hat dort eine Nullstelle ↗
  

• f(x) hat Sattelpunkt ⭢ f'(x) hat Berührpunkt mit der x-Achse (externer Link)
  

• f(x) hat Wendepunkt ⭢ f'(x) hat ein einen Extrempunkt ↗
  

2. Schritt: Steigung dazwischen interpretieren

• Dann ergänzt man zwischen den Punkten den Graphen:
  

• f(x) geht von links nach rechts bergauf ⭢ f'(x) verläuft oberhalb der x-Achse
  

• f(x) geht von links nach rechts bergab ⭢ f'(x) verläuft unterhalb der x-Achse
  

Tipps

• In der Schulmathematik kommen meist nur ganzrationale Funktionen vor.
  

• Für ganzrationale Funktionen gibt es eine einfache Regel:
  

• Mit jedem Ableiten wird der Grad der Funktion um eins kleiner.
  

• Eine kubische (hoch-3) Funktion gibt abgeleitet eine quadratisch Funktion (externer Link)
  

• Eine quadratische Funktion gibt abgeleitet eine lineare Funktion ↗
  

• Eine lineare Funktion gibt abgeleitet eine konstante Funktion ↗
  

• Eine konstante Funktion gibt abgeleitet die Nullfunktion ↗