Epsilon-Umgebung
Analysis
© 2016
- 2025
Definition|
Wofür steht Epsilon hier?|
Was ist eine Umgebung im Sinn der Analysis?|
Was meint Epsilon-Umgebung?|
Worauf kommt es an?|
ε-Umgebung und Extrempunkte|
ε-Umgebung und Grenzwerte|
Fußnoten
Definition
Die Epsilon-Umgebung wird im Zusammenhang mit Grenzwerten (Limes) der Anaylsis definiert. Sie ist ein Intervall um einen Zahlenwert herum, das beliebig klein gedacht werden muss. Erst mit dieser sogenannten Epsilontik konnte der Begriff eines Grenzwertes mathematisch befriedigend definiert werden.
Wofür steht Epsilon hier?
- ε, ausgesprochen als Epsilon meint ein 👉 kleines Epsilon [ε]
- Es steht hier für beliebig klein gedachte aber 👉 positive Zahl
- Positiv meint hier: die Zahl muss größer sein als 0.
- Die 0 selbst gilt nicht als positiv.
- Beispiel: epsilon=0,0004 wäre OK.
Was ist eine Umgebung im Sinn der Analysis?
- Das kleine ε im Sinn der Analysis steht für eine 👉 Umgebung
- Also: der ganze Bereich von etwas weniger als die Zahl...
- bis hin zu etwas mehr als die Zahl.
- Eine Umgebung der 4 wäre etwa: alles von 3,8 bis 4,2.
- Der Bereich hat eine linke und eine rechte Grenze.
- Statt Bereich sagt man oft auch 👉 Intervall
Was meint Epsilon-Umgebung?
- Man spricht konkret von der Epsilon-Umgebung einer Zahl z.
- Das meint: den Bereich von z minus Epsilon bis z plus Epsilon.
- Also alle Zahlen, die zwischen dem linken Rand z minus Epsilon...
- und dem rechten Rand z plus Epsilon liegen.
Worauf kommt es an?
- Das Epsilon deutet an, dass man es beliebig klein machen können muss.
- In Formeln und Lehrsätzen meint das dann, dass eine Aussage immer ...
- auch für beliebige kleine Epsilon-Werte wahr werden oder wahr bleiben muss.
ε-Umgebung und Extrempunkte
- Ein Extrempunkt ist ein Hoch- oder Tiefpunkt auf einem Graphen.
- Ein Punkt ist genau dann ein Extrempunkt, wenn ...
- man zu ihm eine Epsilon-Umgebung angeben kann, ...
- in der es keine höheren oder keine tieferen Punktem gibt.
- Siehe auch 👉 Extrempunkt
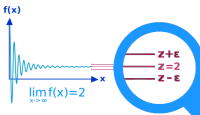
ε-Umgebung und Grenzwerte
- Man hat eine Funktion wie: f(x)=1:x [1]
- Für x gegen unendlich geht ihr Funktionswert gegen 0.
- Die Zahl 0 ist der Grenzwert von f(x) für x gegen unendlich.
- Die Epsilon-Umgebung ist Teil der exakten Definition für einen 👉 Grenzwert
Fußnoten
- [1] Als exakt für den Grenzwert einer Funktion an einer Stelle bezeichnet der Bronstein die folgende Definition: "Damit eine Funktion f(x) an der Stelle x=a einen Grenzwert besitzt, ist es notwendig und hinreichend, dass sich nach Vorgabe einer beliebig kleinen positiven Zahl ε eine zweite positive Zahl η [kleines Eta] angeben lässt, sodass für zwei beliebige Werte x₁ und x₂ aus dem Definitionsbereich, die den Bedingungen |x₁ - a| < η und |x₂ - a < η genügen, die folgende Bedingung erfüllt ist: |f(x₁) - f(x₂) | < ε." In: Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Dort die Seite 55.