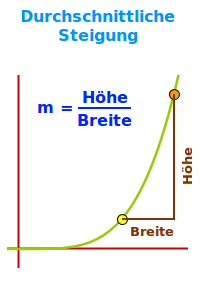
Durchschnittliche Steigung
Graphen
© 2016
- 2025
Definition|
Was meint durchschnittliche Steigung?|
Durchschnittliche Steigung über ein Steigungsdreieck|
Durchschnittliche Steigung als Differenzenquotient|
Alternative Namen der durchschnittlichen Steigung
Definition
Die durchschnittliche Steigung m im Zusammenhang mit einem Graphen ist immer die durchschnittliche Steigung von einem linken Punkt auf dem Graphen zu einem weiter rechts liegenden Punkt auf dem Graphen. Man spricht auch von mittlerer Steigung, mittlerer Änderungsrate, dem Differenzenquotienten oder der Sekantensteigung. Diese durchschnittliche Steigung ist immer auch die Steigung die man erhält, wenn man mit den zwei Punkten die Steigung über ein Steigungsdreieck berechnet. Hier ist die Berechnung kurz erklärt.
Was meint durchschnittliche Steigung?
- Man wählt zwei Punkte auf einem Graphen.
- Man verbindet sie mit einer geraden Strecke.
- (Diese Strecke oder Gerade heißt Sekante.)
- Wenn der Graph zwischen den Punkten gerade wäre, ...
- dann hätte er überall dieselbe Steigung.
- Diese Steigung ist die durchschnittliche Steigung.
- Sie ist identisch mit der Steigung einer Geraden zwischen den zwei Punkten.
- Siehe auch 👉 Steigung aus zwei Punkten
Durchschnittliche Steigung über ein Steigungsdreieck
- Die Grundidee ist die des Steigungsdreiecks.
- Man nimmt zwei verschiedene Punkte auf eine Graphen einer Funktion.
- Mit diesen zwei Punkten zeichnet man ein Steigungsdreieck.
- Dann teilt man die Höhe durch die Breite dieses Dreiecks.
- Das Ergebnis ist die durchschnittliche Steigung.
- Mehr unter 👉 Steigung aus Steigungsdreieck
Durchschnittliche Steigung als Differenzenquotient
- Wenn der linke Punkt (X1|Y1) ist, ...
- und der rechte Punkt (X2|Y2), dann ist ...
- die durchschnittlich Steigung m=(Y2-Y1)/(X2-X1)
- Der Term heißt auch 👉 Differenzenquotient
Alternative Namen der durchschnittlichen Steigung
- Bei Sachaufgaben mit Zeitbezug oft 👉 mittlere Änderungsrate
- Bei geometrischen Überlegungen 👉 Sekantensteigung [ΔY/ΔX]
- Im Zusammenhang mit Ableitung 👉 Differenzenquotient [(Y2-Y1)/(X2-X1)]