Differenzierbar
Eine Funktion kann abgeleitet werden
© 2016
- 2025
Basiswissen|
Was meint differenzieren?|
Was meint differenzierbar anschaulich?|
Notwendige Bedingungen für Differenzierbarkeit|
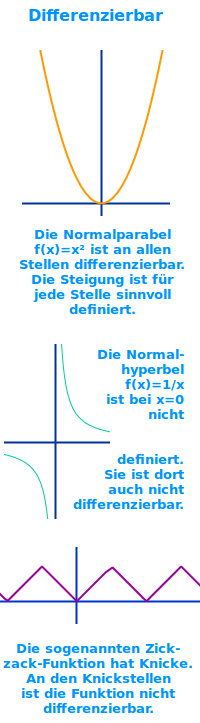
Nicht differenzierbar|
Rechenbeispiel I|
Rechenbeispiel II|
Formale Überprüfung|
Differenzierbare Funktion|
Fußnoten
Basiswissen
Differenzieren ist in der Analysis ein anderes Wort für ableiten, also f'(x) bilden. An Stellen, wo dies für eine Funktion möglich ist, ist die Funktion differenzierbar. Kann man keine erste Ableitung bilden, ist die Funktion dort nicht differenzierbar. Das ist ist hier näher erklärt.
Was meint differenzieren?
- Innerhalb der Mathematik gehört das Wort differenzieren in die 👉 Analysis
- Es hat dort dieselbe Bedeutung wie das Wort ableiten.
- Es meint: die erste Ableitung f'(x) einer Funktion bilden.
- Graphisch meint es: die Steigung eines Graphen ...
- in einem bestimmten Punkt bestimmen.
- Siehe auch 👉 differenzieren
Was meint differenzierbar anschaulich?
- Differenzierbarkeit bezieht sich immer auf einen Punkt auf einem Graphen.
- Es meint: man kann für den Punkt eindeutig eine endliche Steigung angeben.
- Graphisch meint das, dass man dort eindeutig eine Tangente anlegen kann.
- Anschaulich sind das alle Punkte, die keine Lücke oder Knick im Graph sind.
- Lücken oder Knicke im Graphen sind nicht differenzierbare Stellen.
- Bei einer Lücke oder an einem Knick kann man keine eindeutige Steigung angeben.
- Anschaulich heißt differenzieren für einen Punkt auf einem Graphen:
- Es gibt dort eine einzige eindeutige 👉 Tangente
Notwendige Bedingungen für Differenzierbarkeit
- Eine Funktion f(x) ist an einer Stelle xo differenzierbar, wenn sie ...
- a) an dieser Stelle stetig ist und gleichzeitig...
- b) der linksseitige Grenzwert der Tangentensteigung endlich ist und ...
- c) der rechtsseitige Grenzwert der Tangentensteigung endlich ist und ...
- d) der linksseitige Grenzwert der Tangentensteigung gleich dem rechtsseitigen Grenzwert ist.
- Alle vier Bedingungen müssen zusammen gleichzeitig erfüllt sein.
- Ist ein der vier Bedingungen nicht erfüllt, ist f(x) bei xo nicht differenzierbar. [1]
Nicht differenzierbar
- Funktionen mit Knicken oder Lücken sind an diesen stellen nicht differenzierbar.
- Eine Lücke hat z. B. f(x)=1/x an der Stelle x=0, siehe unter 👉 Normalhyperbel
- Knicke hat zum Beispiel die sogenannte 👉 Zickzack-Funktion
Rechenbeispiel I
- Man hat die Funktion: f(x) = x²
- Der Punkt (3|9) liegt auf dem Graphen.
- Was ist die Steigung in diesem Punkt?
- Man leitet f(x) und erhält f'(x)=2x.
- x-Wert dort einsetzen gibt 2·3=6.
- 6 ist die Steigung im Punkt (3|9).
- f(x) war dort als differenzierbar.
Rechenbeispiel II
- Man hat die Funktion: f(x) = 1/x²
- Umgeformt ist das gleich: f(x) = x hoch -2
- Die erste Ableitung f'(x) = -2 mal x hoch -A
- Umgeformt ist das gleich: f'(x) = -2/(x^3)
- Setzt man x=0 ein in f'(x) erhält man: -2/(0)
- Die Division durch 0 ist aber nicht definiert.
- Also kann man für x=0 keine Steigung berechnen.
- f(x) ist an der Stelle x=0 nicht differenzierbar.
Formale Überprüfung
- Man überprüft die Differenzierbarkeit immer an einer Stelle.
- Stelle meint in der Analysis immer einen bestimmten x-Wert.
- Die Funktion muss an dieser Stelle stetig sein.
- Stetig meint: keine Lücke, kein Sprung im y-Wert.
- Und: der linksseitige und der rechtsseitige Grenzwert ...
- für den Differentialquotienten muss die gleiche Zahl ergeben.
- Diese zweite Bedingung meint graphisch: knickfrei.
Differenzierbare Funktion
- Spricht man von einer differenzierbaren Funktionen, ...
- dann meint man damit: dass alle Punkte im Definitionsbereich differenzierbar sind.
Fußnoten
- [1] Definition nach: Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Seite 326.