Anschaulich integrieren

Visuell denken

Basiswissen

Eine einfache Gerade als Beispiel

• Man hat eine Gerade.
  

• Man liest die Funktionswerte graphisch ab und nimmt Überschlagswerte.
  

• Im Beispiel gehe die Gerade vom Punkt (0|-2) bis zum Punkt (4|0,7).
  

• Sie schneidet die x-Achse an der Stelle x=3.
  

• Gesucht ist das Integral von 0 bis 4.
  

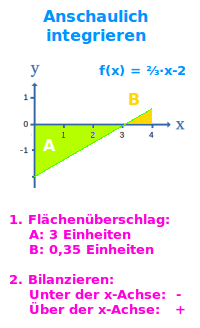
1. Schritt: Teilflächen abschätzen

• Man unterteilt die Gesamtfläche in Teilflächen.
  

• An jeder Nullstelle beginnt eine neue Teilfläche.
  

• Man schätzt die Größe (Flächeninhalt) der ersten Teilfläche.
  

• Man denkt sich dazu ein enges Rechteck um die Fläche gelegt.
  

• Im Beispiel wäre das Rechteck 3 Einheiten breit und 2 Einheiten hoch.
  

• Man kann gut abschätzen, dass das Dreieck dann davon die Hälfte ist.
  

• Die linke Teilfläche unterhalb der x-Achse hat in etwa 3 Flächeneinheiten.
  

• Das rechte Dreieck von x=3 bis x=4 kann man so abschätzen auf etwa 0,35 FE.
  

2.Schritt: Flächenbilanz bilden

• Nun addiert man die zwei Flächeninhalte.
  

• Was unter der x-Achse liegt wird dabei als negative Zahl gedeutet.
  

• Man hat also minus 3 und plus 0,35 Flächeneinheiten, in Summe: -2,65 FE
  

3. Schritt: Antwort formulieren

• Die Flächenbilanz entspricht dem gesuchten Wert des Integrals.
  

• Man kann also als Antwort folgende Abschätzung festhalten:
  

• Der Integralwert liegt bei etwa -2,65.
  

Welchen Sinn gibt ein nicht-sicher-exaktes Ergebnis?

• Bei vielen Fragestellung interessiert nicht der exakte Wert.
  

• Beispiel: man plant eine Windkraftanlage. Sie zu bauen kostet Energie.
  

• Über ihre Lebensdauer wird sie Energie produzieren.
  

• Die prodzierte Energie könnte die positive Fläche sein.
  

• Die investierte Energie wäre dann die negative Fläche.
  

• Es interessiert zunächst: wird die Anlage im Endergebnis ...
  

• mehr Energie produzieren als ihre Errichtung gekostet hat?
  

• Der Überschlag verrät, ob die Planung überhaupt weiterverfolgt werden sollte.
  

• Siehe auch unter Überschlagsrechnung ↗