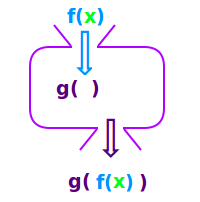
Verkettete Funktion
g∘f = g(f(x))
Der Funktionswert y einer Funktion wird als Argument x in eine andere Funktion eingesetzt. Diese Hintereinanderausführung zweier (oder auch mehrerer) Funktionen nennt man eine Verkettung von Funktion oder auch eine Komposition, man spricht auch von einer zusammengesetzten Funktion [2]. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
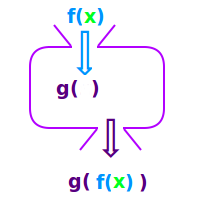Verkettete Funktionen
Beispiele
Der Funktionswert y einer Funktion wird als Argument x in eine andere Funktion eingesetzt. Solche Funktion lassen sich oft einfach mit Hilfe der Kettenregel ableiten. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
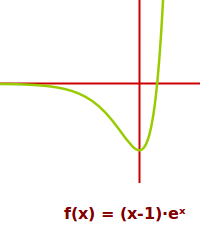Verknüpfte Funktion
Definition
x² und sin(x) werden verknüpftzu x²·sin(x): man hat die Funktionen f(x)=x² und g(x)=e^x. Verbindet man sie über die Multiplikation, erhält man v(x)=x²·e^x. Jede der zwei Funktionen ist damit eine verknüpfte Funktion, die neu entstandene Funktion ist dann die => Verknüpfung
… f(x) abgeleitet gibt f'(x) und heißt => Ableitungsfunktion
Erweiterte e-Funktion
f(x) = a·e^x
f(x) = a·e^x - eine einfache e-Funktion erweitert um einen Faktor. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
