Proportional
Zwei Größen wachsen und schrumpfen miteinander
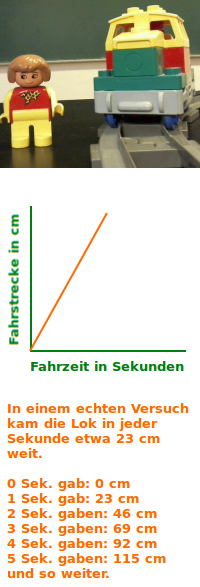
Zwei Größen sind proportional zueinander, wenn eine Verdopplung der einen Größe automatisch auch die andere Größe mit verdoppelt. Beispiel: wenn eine Spielzeuglok doppelt so lange fährt, dann kommt sie auch doppelt so weit. Fahrzeit und Fahrstrecke sind zueinander proportional. => Ganzen Artikel lesen …
Mathematik
Als Proportion [1] oder auch Verhältnisgleichung [6] bezeichnet man zwei Brüche oder zwei Differenzen, die gleichgesetzt wurden [4]. Das ist hier mit Beispielen vorgestellt. => Ganzen Artikel lesen …
… meint dasselbe wie => umgekehrt proportional
Promotion
Erlangung des Doktortitels
Eine Promotion bezeichnet man den Abschluss eines geregelten Verfahrens zur Erlangung des akademisches Doktortitels (englisch: Phd). Eine Promotion kann von einigen Monaten bis zu mehreren Jahren dauern. => Ganzen Artikel lesen …
Definition
Brasilianer mit brauner oder schwarzer Hautfarbe sind im brasilianischen Parlament unterproportional vertreten. Das heißt: der Anteil dunkelhäutiger Personen ist im Parlament kleiner als in der Bevölkerung. Das Wort unterproportional ist hier kurz erklärt. => Ganzen Artikel lesen …
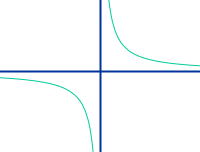
Antiproportionale Funktion
… meint dasselbe wie => umgekehrt proportionale Funktion
… x steht im Nenner, z. B. f(x)=4/x, siehe unter => umgekehrt proportionale Funktion ableiten
Antiproportional heißt dasselbe wie umgekehrt proportional. Die Kernidee zum Ableiten ist, dass 1/x dasselbe ist wie x-hoch-minus-eins: 1/x = x-hoch-minus-eins ⭢ ableiten ⭢ -1 mal x-hoch-minus-zwei. Mehr dazu unter => Umgekehrt proportionale Funktion ableiten
… siehe unter => umgekehrt proportionale Gleichung aus Versuch
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => umgekehrt proportionale Gleichung aus Versuch
Mathematik
Wenn x·y immer gleich 20 sein soll, also x·y=20 gelten soll dann sind x und y zueinander antiproportional. x=2 und y=10 würde hier zum Beispiel die Gleichung lösen. Wenn man nun x doppelt so groß macht, wie es vorher war, und dabei gleichzeitig y halb so groß, dann geht die Gleichung immer noch auf: x=4 und y=5 geben malgerechnet auch 20. Statt antriproportional sagt man auch umgekehrt proportional. Siehe mehr zu diesem Thema im Artikel => umgekehrt proportionale Zuordnung
… meint dasselbe wie => Umgekehrt proportionaler Dreisatz
Mathematik
1 und 6, 2 und 3, 4 und 1,5: zwei Größen sind zueinander indirekt proportional, wenn ihr Produkt (Malrechnung) immer dasselbe Ergebnis ergibt. Das ist ausführlich erklärt im Artikel => umgekehrte Proportionalität
… in der Mathematik dasselbe wie die => Antiproportionalitätskonstante
Mathematik
Bei einer antiproportionalen Zuordnung oder Funktion, auch umgekehrt proportional genannt, ergeben zwei einander zugeordnete Zahlen malgerechnet immer dasselbe Ergebnis. Man spricht auch von Produktgleichheit. Dieses immer gleiche Produkt ist die Antiproportionalitätskonstante. Das ist hier mit einem Beispiel kurz vorgestellt. => Ganzen Artikel lesen …
… Methoden und Aufgaben unter => Proportionalität erkennen über Tabellen
.png "Wie hängen die x-Werte für die Position des Zugblockes oben und die y-Werte für die Höhe des Containers zusammen?")
Containerbruecke (proportional)
Physik
Etwa ab Klasse 3 (mit Anleitung) oder ab Klasse 8 (allein), etwa 10 bis 15 Minuten: ein Containerschiff wird über eine Art Kran, die Containerbrücke be- und entladen. Die Idee dieses Tischversuches ist es, eine Formel zu finden, mit der Kranfahrer auch ohne Sicht auf das Schiff immer wissen, in welcher Höhe ein Container am Kranhaken gerade ist. => Ganzen Artikel lesen …
Mathematik
Man unterscheidet bei Zuordnungen und Funktionen eine direkte und eine indirekte (auch umgekehrte oder anti) Proportionalität. Die direkte Proportionalität gilt dann, wenn man die eine Größe verdoppeln kann und sich die andere dann immer auch verdoppelt. Diese direkte Proportionalität nennt man meist einfach auch nur => Proportionalität
Physik
Mit diesem einseitigen Hebel als Tischversuch kann man einige Eigenschaften einer proportionalen Funktion am Beispiel von Kräften in Newton gemessen betrachten. Umgekehrt propotional zugeordnet sind hier die Entfernung der Bohrung vom Drehpunkt und die nötige Kraft, um den Balken in der Waage zu halten. => Ganzen Artikel lesen …
Fallgeschwindigkeit wächst proportional mit der Falldauer
Von einem Freien Fall spricht man, wenn ein Gegenstand einzig aufgrund der Schwerkraft eines Himmelskörpers nach unten fällt. Vereinfachend geht man dabei normalerweise von einer konstanten Fallbeschleunigung a aus. Für die Erde kürzt man die Fallbeschleunig a oft auch mit g ab. Wir gehen hier auch davon aus, dass zum Beginn des Fallens der Gegenstand keine Geschwindigkeit hatte, also in Ruhe war. Als Faustformel für die Erde gilt: => Ganzen Artikel lesen …
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
Mathematik
1 und 24, 2 und 12, 3 und 8, 4 und 6: zwei Größen sind zueinander indirekt proportional, wenn ihr Produkt (Malrechnung) immer dasselbe Ergebnis ergibt. Das ist ausführlich erklärt im Artikel => umgekehrte Proportionalität
… Methoden und Aufgaben unter => Proportionalität erkennen über Tabellen
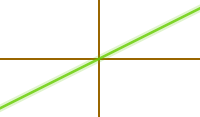
Proportionale Funktion
f(x) = a·x
Jede Funktion, die man in die Schreibweise f(x) = a·x umformen kann heißt proportional. Der Graph ist immer eine Gerade durch den Ursprung (0|0). Jede proportionale Funktion ist immer auch eine lineare Funktion. Der Umkehrschluss gilt aber nicht: nichte jede lineare Funktion ist automatisch auch proportional. => Ganzen Artikel lesen …
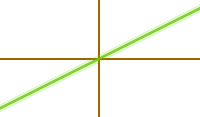
Proportionale Funktion ableiten
f(x)=0,5x wird abgeleitet zu f'(x)=0,5
Als proportional bezeichnet man jede Funktion, die man in die Form f(x)=a·x bringen kann. Dabei ist das a eine beliebige aber immer gleiche Zahl (Konstante). Der Graph einer proportionalen Funktion ist eine Gerade. Eine Gerade hat überall dieselbe Steigung. Also muss auch die Ableitung f'(x) für alle x-Werte denselben y-Wert haben, denn: der y-Wert von f'(x) ist gleich der Steigung von f(x). Man kann jede proportionale Funktion dadurch ableiten, dass man das x im Funktionsterm einfach weglässt. Beispiel: f(x)=255x gibt abgeleitet: f'(x)=255. Siehe mehr zur graphischen Begründung unter => Geradensteigung
… siehe unter => Proportionale Gleichung aus Versuch
Proportionale Funktionen
Beispiele
f(x)=x oder f(x)=4x oder f(x)=0,5x: neben einigen Funktionsgleichungen stehen hier auch Praxisbeispiele: Vulkanausbrüche, Federkonstanten oder praktische Versuche. => Ganzen Artikel lesen …
Proportionale Gleichung
Definition
a=m/x oder a=m:x ist der allgemeine Bauplan für eine porportionale Gleichung: auf einer Seite steht eine Zahl, auf der anderen Seite ein Bruch oder ein Quotient mit dem x im Nenner (unten). Das ist hier kurz definiert. => Ganzen Artikel lesen …
Proportionale Gleichung aus Cosinusdreieck
Versuch
Ein Versuch, wie sich der Cosinus als Verhältnis aus einem realen rechtwinkligen Dreieck ergibt. Hier steht eine Schritt-für-Schritt Anleitung dazu. => Ganzen Artikel lesen …
Proportionale Gleichung aus Versuch
Liste
Verschieden Versuche von etwa 10 bis 30 Minuten Dauer betrachten verschiedene Aspekete der Proportionalität. Der Hintergrund ist technisch bis naturwissenschaftlich. => Ganzen Artikel lesen …
Beispiele
4 = 2x: auf einer Seite steht eine Zahl, auf der anderen Seite ein Buch oder ein Quotient. Hier stehen einige Beispiele für solche proportionalen Gleichungen. => Ganzen Artikel lesen …
Tipps
10·x = 80: auf einer Seite einer Gleichung steht ein Bruch oder ein Quotient, auf der anderen Seite steht eine Zahl. In Anlehnung an eine proportionale Funktion kann man solche Gleichungen als proportional bezeichnen. Hier stehen Tipps zur Lösung. => Ganzen Artikel lesen …
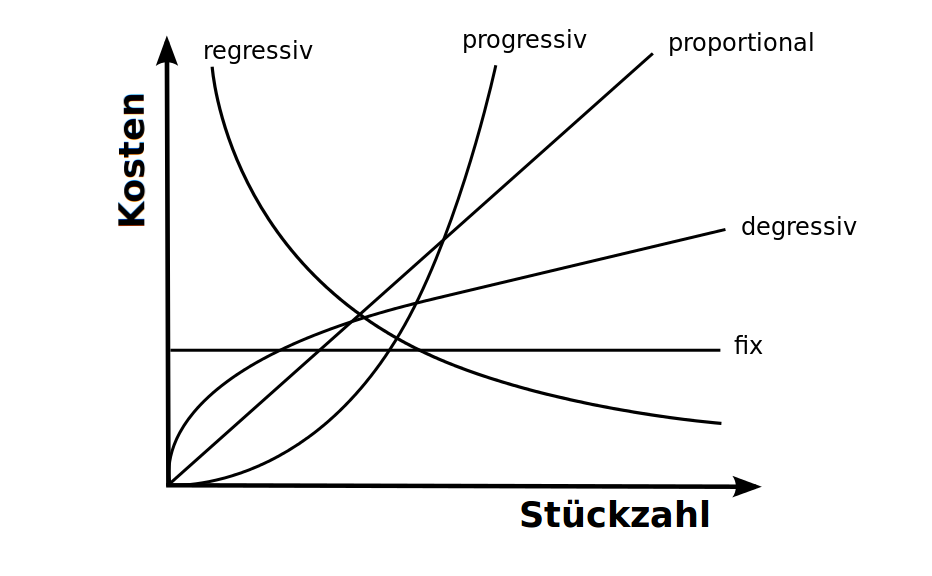
Proportionale Kostenfunktion
Wirtschaft
Die Gesamtkosten sind proportionale zur Stückzahl. Das ist hier kurz definiert. => Ganzen Artikel lesen …
