Null hoch

Entweder 0 oder nicht definiert

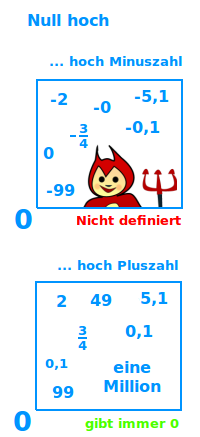
0³ ist ausgeschrieben: 0·0·0. Das gibt ausgerechnet genau 0. Man kann verallgemeinern und sagen: 0 hoch eine positive Zahl gibt immer 0. Anders sieht es aus, wenn der Exponent negativ oder die 0 selbst ist. => Ganzen Artikel lesen …

4: Null hoch x

… ist nur definiert für positive Zahlen, siehe auch => hoch null

5: Nur hoch

… nie bergab in der Mathematik, siehe => Monoton steigend

6: Neun hoch

… 9² gibt 81: Malketten nur mit Neunern, siehe auch => Neunerpotenzen

7: Null hoch -2

… warum das nicht definiert ist, siehe unter => Null hoch minus zwei

9: Kleiner Null hoch irgendwas

… so etwas wie (-3)³, siehe unter => Negative Zahlen potenzieren

12: 0 hoch 1

… ist genau 0. Siehe unter => null hoch

14: Null hoch irgendwas

… ist entweder 0 oder nicht definiert, mehr unter => hoch null

15: Null hoch minus

… egal was ist nicht definiert, mehr unter => Null hoch minus eins

16: Null hoch minus 1

… ist nicht definiert, warum steht unter => Null hoch minus eins

17: Null hoch minus 2

… warum das nicht definiert ist, siehe unter => Null hoch minus zwei

18: Null hoch minus drei

… ist nicht definiert, geht nicht, siehe auch => hoch null

20: Null hoch minus irgendwas

… ist nicht definiert, mehr unter => Null hoch minus eins

23:

Null hoch null

0° = ↯

Irgendwas hoch null gibt immer 1, mit einer Ausnahme: 0 hoch 0 ist nicht definiert. Taschenrechner geben für den Term 0^0 üblicherweise eine Fehlermeldung wie „Error“ oder „Kein mathematischer Ausdruck aus“. Siehe auch unter => nicht definiert

28: 0 hoch 2

… ist genau 0, lies mehr unter => Null hoch

29: Zahl kleiner Null hoch

… z. B. (-2)³, siehe unter => Negative Zahlen potenzieren