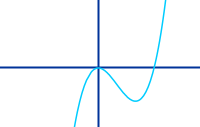
Kubische Funktion ableiten
Anleitung
f(x) = x³-8x²-5x+2 gibt f'(x) = 3x²-16x-5: eine kubische Funktion wird oft auch ganzrationale Funktion dritten Grades genannt. Die höchste Potenz von x ist die Zahl 3. Bei der Ableitung entsteht immer eine quadratische Funktion. Das Ableiten ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
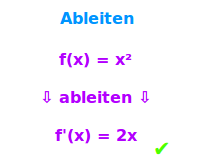Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
Anleitung
f(x) = 2x⁴+4x³-5x²+8x-20 wird abgeleitet zu f'(x) = 8x³-10x+8: Eine quartische Funktion wird oft auch ganzrationale Funktion vierten Grades genannt. Die höchste Potenz von x ist die Zahl 4. Bei der Ableitung entsteht immer eine kubische Funktion (hoch 3). Das ist hier an einem Zahlenbeispiel erklärt. => Ganzen Artikel lesen …
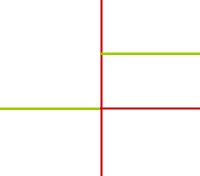Heaviside-Funktion ableiten
Wie man die erste Ableitung f'(x) bildet
Die Heaviside-Funktion ist links von der y-Achse identisch mit der x-Achse. Für x>0 und auch x=0 selbst ist der Graph eine horizontale Gerade parallel zur x-Achse mit y=1. Diese Funktion hat überalle die Steigung 0, also ist auch f'(x) überall 0. Lediglich an der Stelle x=0 hat die Funktion eine Sprungstelle und ist deshalb dort nicht ableitbar. Diese Gegebenheiten sind im Folgenden noch einmal zusammengefasst: => Ganzen Artikel lesen …
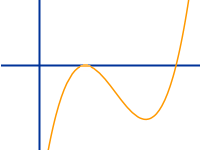Kubische Funktionen
Arten und Beispiele
Reinkubisch, gemischtkubisch sowie ohne und mit absolutem Glied: hier stehen einige wichtige Arten kubischer (hoch drei) Funktionen sowie dazu auch konkrete Beispiele mit Zahlenwerten. => Ganzen Artikel lesen …
Anleitung
f(x)=4x²+2x-5 wird abgeleitet zu f'(x)=8x+2: eine quadratische Funktion f(x) ergibt abgeleitet immer eine lineare Funktion. Die Lösungsidee zum Ableiten besteht darin, die Glieder des Funktionstermes einzeln abzuleiten. Das wird hier an einem Beispiel gezeigt. => Ganzen Artikel lesen …
