Konkav
Optik, Geometrie
Konkav heißt: irgendwo auch nach innen gewölbt. Der Begriff wird sowohl für Linsen in der Optik als auch für 2D- und 3D-Figuren in der Geometrie verwendet. => Ganzen Artikel lesen …
Bikonkav
)(
Beide Seiten sind nach innen gewölbt (gehöhlt): bikonkav nennt man Linsen, deren Hauptflächen beide nach innen gewölbt sind, sozusagen schüsselförmig eingedellt. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Donau
Fluß mit den meisten Ländern der Welt
Die Donau ist mit einer mittleren Wasserführung von rund 6855 Kubikmetern in jeder Sekunde und einer Gesamtlänge von 2857 Kilometern nach der Wolga der zweitgrößte und zweitlängste Fluss in Europa. Sie hat ihre Quelle im südlichen Schwarzwald. Die Donau durchfließt zehn Länder (Deutschland, Österreich, Slowakei, Ungarn, Kroatien, Serbien, Bulgarien, Rumänien, Moldawien und Ukraine) - so viele wie kein anderer Fluss auf der Erde. => Ganzen Artikel lesen …
Eckig
Hexagon oder diagonal: als Teil eines anderen Wortes angefügt, hat gonal oft die Bedeutung von Eckigkeit. Hier sind einige Fälle kurz vorgestellt. => Ganzen Artikel lesen …
|( eine Seite ist flach (plan), die andere nach innen gewölbt.
Das Wort Plankonkav wird meist in Verbindung mit optischen Linsen verwendet. Eine Linse ist dann plankonkav, wenn sie auf einer Seite ganz flach und auf der anderen Seite nur nach innen gewölbt ist. Plankonkav ist damit ein Sonderfall von konkav. Eine konkave Linse, und damit auch eine plankonkave Linse ist von der optischen Wirkung her immer eine => Zerstreuungslinse
Konvex
Optik, Geometrie
Konvex heißt: nur nach außen gewölbt, nie nach innen. Der Begriff wird sowohl für Linsen in der Optik als auch für 2D- und 3D-Figuren in der Geometrie verwendet. => Ganzen Artikel lesen …
)( Auf beiden Seiten nach innen gewölbt
Eine Bikonkave Linse ist nach beiden Seiten hin nach innen gewölbt. Sie ist von der Funktion her immer eine => Zerstreuungslinse
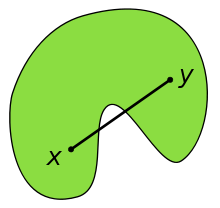Konkave Figur
Geometrie
Eine konkave Figur ist immer etwas flächiges (2D). Eine Figur heißt konkav, wenn man zwei Punkte auf ihrem Rand finden kann, bei denen die geradlinige Verbindungsstrecke irgendwo auch außerhalb der Figur verläuft. Ein typisches Beispiel ist die => konkave Linse
Beispiele
Konkave Figuren haben an ihrer Oberfläche eine nach innen gehende Wölbung. Man kann zwei Punkte auf der Oberfläche finden, deren gerade Verbindungsstrecke zumindest teilweise außerhalb der Figur verläut. Das stehen hier Beispiele. => Ganzen Artikel lesen …
Analysis
In der Analysis spricht man von konvexen und konkaven Funktionen. Um eine Funktion auf Konkavität zu prüfen, kann man sich ihren Graphen betrachten. Man denkt sich zwei gerade Verbindungsstrecken zwischen zwei beliebigen Punkten der Kurve. Liegen alle Punkte des Graphen dann oberhalb jeder solchen Verbindungsstrecke, heißt die Funktion konkav. [1] => Ganzen Artikel lesen …
Konkave Linse
Nie nach außen gewölbt, aber nach innen
Eine konkave Linse ist an mindestens einer Seite nach innen gewölbt. Ist sie auf beiden Seiten nach innen gewölbt, nennt man sie auch bikonkav. Eine konkave Linse ist von der optischen Wirkung her immer eine => Zerstreuungslinse
Konkaver Körper
Vertiefungen
Ein konkaver Körper kann gerade oder auch gebogene und geschwungene Begrenzungsflächen und -ebenen haben. Wenn es mindestens zwei Punkte auf der Oberfläche eines solchen Körpers gibt, bei der die kürzeste Verbindungsstrecke zumindest teilweise außerhalb des Körpers verläuft nennt man den Körper => konkav
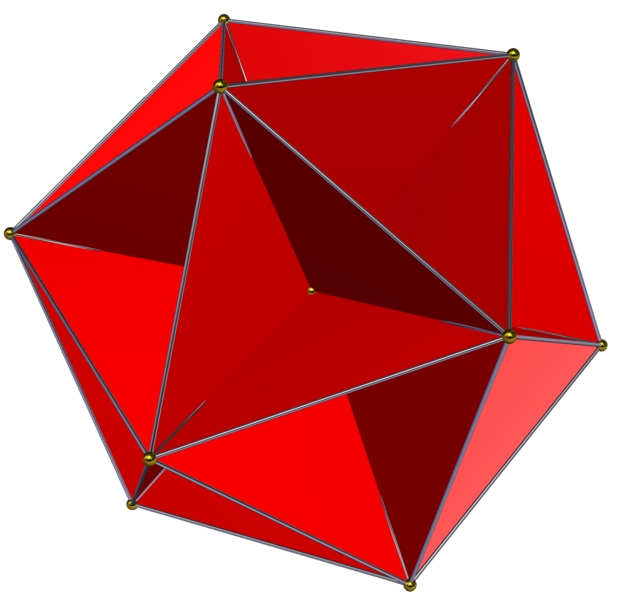Konkaves Polyeder
Vertiefungen
Ein konkaves Polyeder ist ein Körper, der ausschließlich ebene Flächen als Begrenzung hat. Alle seine Kanten sind nur gerade Strecken. Konkav heißt so ein Körper, wenn es mindestens zwei Punkte auf der Oberfläche eines solchen Körpers gibt, bei der die kürzeste Verbindungsstrecke zumindest teilweise außerhalb des Körpers verläuft. Siehe auch => konkav
Konkaves Viereck
Viereck mit Einbuchtung
Konkav heißt so viel wie nach innen gewölt, hohl (englisch: cave), mit einer Mulde. Ein konkaves Viereck sieht so aus, als sein eine Ecke nach innen gedrückt. Mathematisch gesprochen heißt das, dass mindestens ein Innenwinkel größer ist als 180 Grad. Ein konkaves Viereck ist ein Sonderfall einer konkaven Figur. Siehe auch => konvexes Viereck
|( Auf einer Seite flach, auf der anderen nach innen gewölbt
Eine plankonkave Linse ist auf einer Seite flach (plan) und auf der anderen nach innen gewölbt (ausgehöhlt: englisch cave=Höhle). Sie ist von der Funktion her immer eine => Zerstreuungslinse
