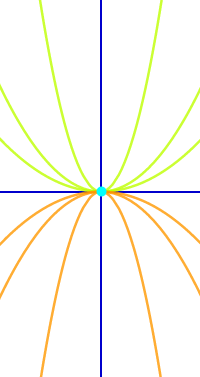
Gemeinsamen Punkt einer Kurvenschar berechnen
Anleitung
Man hat eine Kurvenschar gegeben. Die Schar besteht aus theoretisch unendlich vielen Graphen. Manchmal, aber nicht immer, gehen alle Graphe einer Schar durch einen gemeinsamen Punkt. Hier steht, wie man diesen gemeinsamen Punkt berechnet (wenn es ihn gibt). => Ganzen Artikel lesen …
Mathematik
Dezimalpunkt, Tausendertrennpunkt und Multiplikations-Punkt: diese drei wichtigen Bedeutungen sind hier kurz erklärt. Viele weitere Bedeutungen stehen unter => Punkte
Ganze Zahlen
Einer sind die Zahlen aus der Einerreihe: 0; 1; 2; 3; 4 und so weiter. Nicht zu den Einern zählen echte Kommazahlen wie 3,4 sowie auch Brüche deren Wert nicht ganzzahlig ist, etwa 3/4 oder 5/9. Einer dürfen aber negativ sein, wie etwa -17 oder -16. => Ganzen Artikel lesen …
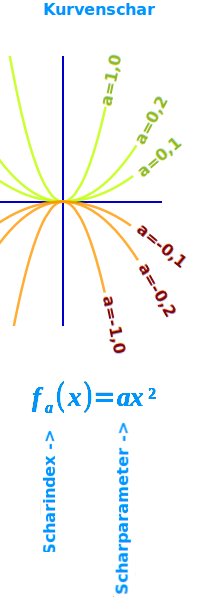=> Funktionsschar
=> Gemeinsamen Punkt einer Kurvenschar berechnen [mit qck]
=> nach unten geöffnet
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
… siehe unter => gemeinsamen Punkt einer Kurvenschar berechnen
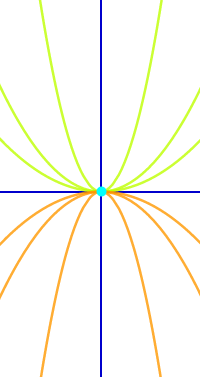Gemeinsamer Punkt einer Kurvenschar
Analysis
Punkt, durch den alle Graphen der Schar gehen: alle Graphen einer Schar gehen durch einen einzigen oder mehrere gemeinsame Punkt. Das wird hier kurz erklärt. => Ganzen Artikel lesen …
… Rechenbeispiel unter => Ortslinie einer Kurvenschar berechnen
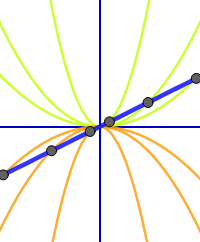Ortslinie einer Kurvenschar berechnen
Anleitung
Zum Beispiel: alle Punkte einer Schar, die die Steigung 1 haben oder alle Tiefpunkte können auf einer gemeinsamen Linie liegen. Eine solche Linie, die Punkte gemeinsamer Eigenschaften verbindet heißt Ortslinie. Es wird Schritt für Schritt die Berechnung erklärt. => Ganzen Artikel lesen …
