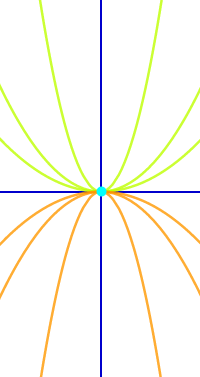
Gemeinsamen Punkt einer Kurvenschar berechnen
Anleitung
© 2016
- 2025
Basiswissen
Man hat eine Kurvenschar gegeben. Die Schar besteht aus theoretisch unendlich vielen Graphen. Manchmal, aber nicht immer, gehen alle Graphe einer Schar durch einen gemeinsamen Punkt. Hier steht, wie man diesen gemeinsamen Punkt berechnet (wenn es ihn gibt).
Verfahren
- Der Scharparameter sei hier a genannt.
- Ein gemeinsamer Punkt muss für unterschiedliche Parameterwerte gelten.
- Das heißt, zum Beispiel für a=3 und a=4 muss es einen Punkt mit gleichem x- und y-Wert geben.
- Das formuliert man mathematisch allgemein so:
- f(x) mit Parameter a muss gleich f(x) mit Parameter b sein.
- Man setzt die zwei Funktionsterme dann gleich.
- Durch die Gleichsetzung entsteht eine Gleichung mit a, b und x aber ohne y.
- Man löst diese Gleichung nach x auf. Dabei kann man a und b eliminieren.
- Eliminieren meint hier: es gibt eine Umformung durch die a und b verschwinden.
- Beispiel: x(2a-2b)=0
- Wenn - wie gefordert - a und b unterschiedlich sind, dann ...
- ist der Klammerterm immer auch ungleich 0.
- Man darf dann also auf beiden Seiten durch den Klammerterm teilen.
- Genau durch diese Äquivalenzumformung verschwinden mit der Klammer a und b.
- Verschwinden a und b, dann gibt es einen gemeinsamen Punkt, ansonsten nicht.
- Den Term für den x-Wert setzt man in f(x) mit beliebig gewähltem Parameterwert ein.
- Das ist der y-Wert.
Beispiele
fₐ(x)=ax²
- Gegeben ist die Schar: fₐ(x)=ax²
- Parameter a und b unterscheiden und 👉 gleichsetzen
- ax²=bx²| In Nullform bringen
- ax²-bx²=0
Nullform heißt hier, dass eine Gleichung auf einer Seite des Gleichheitszeichens nur die Zahl 0 hat. Die Nullform bringt oft den Vorteil, dass man die andere Seite durch Faktorisieren zu einer Malkette (Produkt) macht. Und dann kann man den Satz vom Nullprodukt anwenden:
- ax²-bx²=0 | jetzt x² ausklammern, also 👉 faktorisieren
- x²(a-b)=0 | 👉 Satz vom Nullprodukt
- Gleichung geht auf, wenn x=0 ist oder a und b gleich sind.
- Dass a und b gleich sind, wurde am Anfang verboten.
Dies ist eine wichtige Stelle im Verfahren: rein rechnerisch würde die Gleichung aufgehen, wenn a und b den gleichen Zahlenwert hätten. Anschaulich im Sinne der Schar würde das aber heißen, dass man zweimal denselben Graphen hat. Und weiter gedacht hieße dass, einen gemeinsamen Punkt gibt es nur, wenn die Graphen dieselben Graphen sind. Für verschiedene Werte des Parameters gäbe es dann keinen gemeinsamen Punkt. Damit gäbe es aber auch gar keinen gemeinsamen Punkt für verschiedene Graphen, eine Lösung, die nicht gewollt ist oder nicht interessiert. Man schließt also die Lösung für m=n aus und sucht weiter nach möglichen x-Werten für einen gemeinsamen Punkt mit unterschiedlichen Werten m und n für den Parameter:
- Wir betrachten weiter: x²(a-b)=0
- Die zweite Lösung der Gleichung wäre, dass x=0 ist.
- Das ist also der x-Wert des gemeinsamen Punktes.
- Einsetzen in f(x) liefert den y-Wert: 0
- Also ist der gemeinsame Punkt: (0|0)
Um das Ergebnis zu kontrollieren, kann man mehrere Graphen der Schar fₐ(x)=ax² zeichnen. Man setzt dazu für a verschiedene Werte ein und zeichnet für jeden einzelnen Wert den Graphen. Man wird sehen, dass alle diese Graphen durch den Koordinatenursprung (0|0) als gemeinsamen Punkt gehen.
fₘ(x)=2mx²+4mx+5
Die Schar fₐ(x)=2mx²+4mx+5 besteht aus einzelnen quadratischen Funktionen die alle durch die Punkte (-2|5) und (0|5) als gemeinsame Punkte gehen. Das Beispiel zeigt, dass es auch mehr als einen gemeinsamen Punkt geben kann. Sehen wir, wie diese zwei Punkte aus der formalen Rechnung auch herauskommen.
- Gegeben ist die Schar: fₐ(x)=2mx²+4mx+5
- Parameter m und n unterscheiden und 👉 gleichsetzen
- 2mx²+4mx+5=2nx²+4nx+5 | -5 als Vereinfachung
Die +5 am Ende des Funktionstermes ist ein sogenantes absolutes Glied, ein Term ohne Variable. Solche absoluten Glieder fallen bei der Umformung nach x immer weg. Das macht anschaulich Sinn, da absolute Glieder den Graphen nur nach oben der unten verschieben. Eine solche Verschiebung hat aber keinen Einfluss auf den x-Wert von gemeinsamen Punkten. Der Formalismus wird dem gerecht, indem die entsprechenden Glieder bei der Umformung verschwinden.
- 2mx²+4mx=2nx²+4nx | in Nullform bringen:
- 2mx²+4mx-2nx²-4nx=0 | 👉 Quadratische Gleichung
Die Variable x kommt hier mit ihrem Quadrat vor, man hat hier eine quadratische Gleichung. Da quadratische Gleichungen bis zu zwei Lösungen haben können, kann man hier schon vermuten, dass es auch bis zu zwei gemeinsame Punkte der Schar geben kann. Zur weiteren Umformung im Sinne eines Auflösens nach x könnte man ab hier verschiedene Verfahren (Faktorisieren, pq-Formel etc.) wählen. Gibt es kein absolutes Glied mehr in der Gleichung, ist das Faktorisieren hin zum Satz vom Nullprodukt oft der einfachste Weg:
- (2m-2n)x²+(4m-4n)x=0 | 👉 Faktorisieren
- x·[(2m-2n)x+(4m-4n)]=0 | 👉 Satz vom Nullprodukt
- x=0 ist die erste Lösung
- Einsetzen von 0 in f(x) liefert den y-Wert: 5
Der erste gemeinsame Punkt ist also bei (0|5). Nach dem Satz vom Nullprodukt kann man sich jetzt den zweiten Faktor der Malkette links vom Gleichheitszeichen alleine betrachten. Damit hat man keine quadratische Gleichung mehr sondern eine nur noch lineare Gleichung. Diese kann man nach x auflösen:
- (2m-2n)x+(4m-4n)=0 | :2 als Vereinfachung
- (m-n)x+(2m-2n)=0 | m-n ausklammern
- (m-n)(x+2)=0 | durch m-n
Wieder muss man hier im Hinterkopf behalten, dass die Division durch m-n nur dann erlaubt ist, wenn m und n verschieden sind. Wären sie gleich, wäre der Term vom Wert her eine 0 und man würde dann durch 0 teilen. Das ist aber mathematisch nicht definiert. In der Denkweise einer Kurvenschar heißt die Forderung, dass m und n verschieden sind anschaulich gesprochen, dass man zwei verschiedene und nicht zweimal denselben Graphen der Schar betrachtet. Also teilen wir durch m-n:
- (m-n)(x+2)=0 | durch m-n
- x+2=0 | -2
- x=-2
- Einsetzen von -2 in f(x) liefert den y-Wert: 5
Der zweite gemeinsame Punkt der Schar ist also (-2|5). Um das Ergebnis strichprobenartig zu kontrollieren, kann man verschiedene Graphen der Schar zeichnen. Man wird sehen, dass sie alle durch die zwei gefundenen Punkte gehen.
Aufgaben mit Lösungen
- a) fₐ(x) = a x + 1 − a
- b) fₐ(x) = a x + 3 − 2a
- c) fₐ(x) = a x + 2
- d) fₐ(x) = a (x − 1)² + 2
- e) fₐ(x) = (x − 2)² + a (x − 2) + 5
- f) fₐ(x) = a x² + (1 − a) x
- g) fₐ(x) = a (x − 1)³ + 7
- h) fₐ(x) = a (x − 3)³
- i) fₐ(x) = a e^x + 2 − a
- j) fₐ(x) = a 2^(x − 1) + 5 − a
Lösungen: a(1,1), b(2,3), c(0,2), d(1,2), e(2,5), f(1,1), g(1,7), h(3,0), i(0,2), j(1,5). Überprüfe die Lösungen mit stichprobenartig gezeichneten Graphen mit verschiedenen Werten für den Parameter.