Methoden
f(x)=4x³-3x²+4x-22 wird zu f'(x)=12x²-6x+4: ganzrational nennt man zum Beispiel die linearen, quadratischen und kubischen Funktionen. Hier stehen Regeln und Sonderfälle zum Ableiten einer ganzrationalen Funktion. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
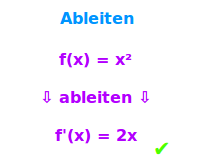Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
Beispiele
Lineare und quadratische Funktionen sind typische ganzrationale Funktion. Hier steht mit Beispielen kurz erklärt wie man solche Funktionen aufleitet. => Ganzen Artikel lesen …
Wie man die erste Ableitung bildet
Rational meint im Kontext von Funktionsgleichungen dasselbe wie gebrochenrational: Der Funktionsterm ist ein Quotient aus zwei ganzrationalen Funktionen. Beispiel: f(x) = (4x^2 + 2x + 3):(x^14 + x^9 - 3). Wie man solche Funktionen ableitet ist erklärt unter => gebrochenrationale Funktion ableiten
Ganzrationale Funktionen
Systematik
Als ganzrational bezeichnet man alle Funktionen, die man in einen gemeinsamen Bauplan umformen kann: (x) = aₙ·xⁿ + aₙ₋₁·xⁿ⁻¹ + + a₂·x² + a₁·x¹ + a₀. Ganzrationale Funktionen spielen eine herausragende Rolle in der Schulmathematik. Ihre Systematik folgt dem höchsten Exponent (der größten Hochzahl) der Variablen x. => Ganzen Artikel lesen …
