Eindimensionale Funktion
y = f(x)
Eine eindimensionale (reellwertige) Funktion ist eine Abbildung von einer Teilmenge D ⊂ R in eine Teilmenge T ⊂ R der reellen Zahlen [1]. Typisch dafür ist die Funktion f(x), die jedem x-Wert genau einen y-Wert zuordnet. Die Dimensionalität bezieht sich hier auf die Anzahl der unabhängigen Variablen. Unabhängig nennt man die Variablen, für die man Werte einsetzt, hier also das x. Die verkürzte Bezeichnung Funktion steht meist für eine eindimensionale Funktion. Lies mehr dazu unter => Funktion
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
Dreidimensionale Funktion
z=f(w,x,y)
Dreidimensionale Funktionen haben genau drei unabhängige Variablen, zum Beispiel als w, x und y bezeichnet. Sie werden in die Funktionsgleichung eingesetzt und ergeben dadurch den Wert der abhängigen Variablen, oft z genannt. Dreidimensionale Funktion haben also vier Variablen. Sie werden oft in einem 3D-Koordinatensystem mit Dichtewolken oder Farbstufungen dargestellt. Das ist hier kurz erläutert. => Ganzen Artikel lesen …
z=f(v,w,x,y)
Vierdimensionale Funktionen haben genau vier unabhängige Variablen, z. B. als v, w, x und y bezeichnet. Sie werden in die Funktionsgleichung eingesetzt und ergeben dadurch den Wert abhängigen Variablen, oft z genannt. Der Graph einer solchen Funktion kann nicht mehr alleine über Punktorte dargestellt werden. => Ganzen Artikel lesen …
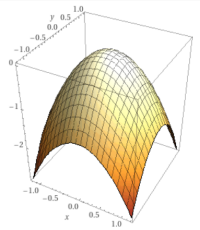Zweidimensionale Funktion
z=f(x;y)
Die Dimension einer Funktion entspricht der Anzahl der unahbängigen Variablen: zweidimensionale Funktionen, auch als Funktionen mit zwei veränderlichen [2], mit zwei Variablen [3] oder als bivariate Funktionen bezeichnet [3], haben dementsprechend genau zwei unabhängige Variablen, oft als x und y bezeichnet. Die dritte Variable, oft das z, ist von x und y abhängig und heißt auch Funktionsargument. Das ist hier näher erläutert. => Ganzen Artikel lesen …
Beispiele
Als zweidimensional bezeichnet man Funktionen, die zwei Argumente haben, also zwei Zahlen, die man in den Funktionsterm einsetzt. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
