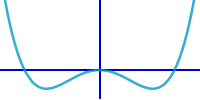
Biquadratische Funktion
f(x) = ax^4 + bx^2 + c
Eine Funktion mit x hoch 4 und x hoch 2 nennt man biquadratisch. Diese Funktion und ihre Berechnungen werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
Beispiele
f(x) = 2x⁴ - 8x² + 16 - bei einer biquadratischen Funktion gibt es im Funktionsterm ein x⁴ sowie immer auch ein x². Daneben kann es - muss aber nicht - noch ein absolutes Glied geben, das heißt eine Zahl ohne x. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
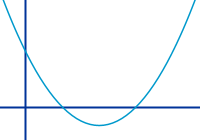Quadratische Funktion
f(x)=ax²+bx+c
Jede Funktion deren Gleichung man auf die Form f(x)=ax²+bx+c bringen kann heißt quadratisch. Das a darf irgendeine Zahl außer der Null sein. b und c dürfen auch - müssen aber nicht - Null sein. Der dazugehörige Graph ist immer eine (quadratische) Parabel. => Ganzen Artikel lesen …
Reinquadratische Funktion
f(x) = ax² + c
Der Funktionsterm hat immer ein quadratisches Glied (etwas mit x-quadrat). Dahinter darf - muss aber nicht ein + oder - mit absolutem Glied (eine reine Zahl ohne x) folgen. => Ganzen Artikel lesen …
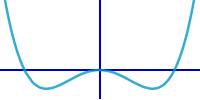Biquadratische Funktion ableiten
Zum Beispiel f(x) = 2x^4-5x^2+6 ableiten gibt f'(x) = 8x³-10x
Als biquadratisch Funktion bezeichnet man eine ganzrationale Funktion vierten grades (quartische Funktion) mit ausschließlich geraden Exponenten von x. Eine biquadratische Funktion hat die allgemeine Form f(x) = ax^4 + bx^2 + c. Durch Umformung kann man jede biquadratische Funktion in diese Form bringen. Sie kann dann mit Hilfe der Faktor- und der Potenzregel abgeleitet werden. => Ganzen Artikel lesen …
… siehe => Nullstellen von biquadratischen Funktionen bestimmen
… siehe => Nullstellen von biquadratischen Funktionen bestimmen
… siehe => Nullstellen von biquadratischen Funktionen bestimmen
… siehe => Nullstellen von biquadratischen Funktionen bestimmen
… siehe => Nullstellen von biquadratischen Funktionen bestimmen
… siehe => Nullstellen von biquadratischen Funktionen bestimmen
x^4 und x^2
f(x) = x⁴-x²-12: eine Funktion, bei der das x sowohl hoch vier wie auch hoch zwei gerechnet wird und am Ende noch eine reine Zahl addiert oder subtrahiert wird. Für diesen Sonderfall einer quartischen (hoch vier) Funktion lassen sich die Nullstellen über Substitution vergleichsweise einfach berechnen. => Ganzen Artikel lesen …
