Anleitung
f'(x) = 1:(f⁻¹)' abgeleitet. Diese Regel nennt man Inversenregel oder auch Umkehrregel. Sie ist hier kurz an einem Beispiel erklärt. => Ganzen Artikel lesen …
Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… der Differentialrechnung, siehe unter => ableiten über Umkehrregel
Anleitung
f(x) = 2·x³ wird abgeleitet zu f'(x) = 2·3·x². Der Faktor hier ist die Zahl 2 vor dem x³. Die allgemeine Regel dazu ist: a·g(x) ableiten gibt a·g'(x). Das heißt: ein konstanter Faktor a, der mit einem Term multipliziert wird, der x enthält, bleibt beim Bbleiten erhalten. Konstante Faktoren sind zum Beispiel alle reinen Zahlen und alle Terme, die man auf eine Zahl hin zusammenfassen kann. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Anleitung
f(x) = x² + 4x gibt abgeleitet f'(x) = 2x+4: die allgemeine Regel ist, dass man die Teile einer Plus- oder Minuskette, im Prinzip also die Summanden, für sich einzeln ableiten kann. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
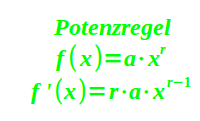Ableiten über Potenzregel
x² ⭢ 2x¹
x² gibt 2·x¹ oder kurz nur 2x: Exponent als Faktor runterziehen und eins kleiner machen. Beispiel: bei x³ ist der Exponent die Zahl 3. Diesen als Faktor (Malzahl) vor das x ziehen und dann den alten Exponenten eins kleiner machen: 3x². Als Regel: xʳ abgeleitet gibt r·xʳ⁻¹. Mehr unter => Potenzfunktion ableiten
Ableiten über Kettenregel
Analysis
Die Funktion f(x)=(4x+2)³ gibt abgeleitet 4·3·(4x+2)². Die verwendete Regel war als Merkspruch: innere Ableitung (das gab hier die Zahl 4) mal äußerer Ableitung (das gab das 3·(4x+2)². Das wird hier kurz vorgestellt. => Ganzen Artikel lesen …
