Geometrie
Eine Verschiebung ist eine Lageänderung ohne Änderung der Form oder Größe und auch ohne Drehung: verschiebt man einen Körper, Graphen oder Fläche, wird dabei weder die Form noch die Größe verändert. Auch darf keine Drehung stattfinden. Das Fremdwort für Verschiebung ist Translation. Hier stehen Beispiele für Figuren und Vektoren. => Ganzen Artikel lesen …
Bedeutungen in der Mathematik
In der Mathematik werden Graphen oft verschoben. Meistens parallel zur x-Achse (links/rechts) oder parallel zur y-Achse (oben/unten). Mehr unter => Graphen transformieren
Astronomie
Als Rotverschiebung bezeichnet man heute die „Rotfärbung des Lichtes eines Sternes, der sich von uns fortbewegt, infolge des Doppler-Effektes.“ [1] Dass weiter entfernte Himmelskörper rötlicher erscheinen war seit spätestens 1914 bekannt [9], wennauch die genaue Ursache noch unklar war [10]. Die heute noch laufende Debatte, ob der Amerikaner Hubble oder der Belgier Lemaitre als Urheber der Erkenntnis gelten dürfen, verschiebt sich anhand eindeutiger Quellen um mindestens ein Jahrzehnt weiter Richtung Vergangenheit und hin zu andere Autoren. => Ganzen Artikel lesen …
Geologie
Eine geologische Überschiebung ist der Prozess oder das Ergebnis von einer Aufschiebung eines Gesteins- oder Sedimentpaktes auf ein anderes. Dadurch können ältere Schichten oben auf jüngere Schichten aufgeschoben werden. Üblicherweise liegen jüngere Schichten immer weiter oben. Siehe dazu auch => stratigraphisches Prinzip
… siehe unter => Graphen verschieben
Bewegung der Kontinente
Wenige Millimeter bis zu knapp 20 Zentimeter in einem Jahr: so schnell bewegen sich die Kontinente der Erde zueinander. Dieses Phänomen nennt man Kontinentalverschiebung oder auch => Kontinentaldrift
… z. B. verschieben oder stauchen => Graphen transformieren
Übersicht
Nach oben und unten sowie nach links und nach rechts: Parabeln als Graphen einer quadratischen Funktionen kann man vergleichsweise leicht parallel zu den Koordinatenachsen verschieben. Die vier Grund-Methoden dazu sind hier kurz vorgestellt. => Ganzen Artikel lesen …
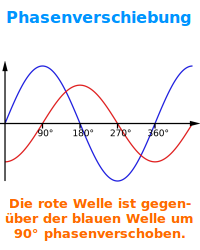Phasenverschiebung
φ Physik
Wie stark zwei Wellenzüge gegeneinander verschoben sind: die Verschiebung wird oft als Winkel angegegeben. Die übliche Abkürzung ist dann das kleine griechische phi. Mehr dazu unter => Phasenwinkel
… z. B. verschieben oder stauchen => Graphen transformieren
… siehe unter => Parabeltransformationen
… für lineare Funktionen => Verschiebungsform der Geradengleichung
… als lineare Funktion => Verschiebungsform der Geradengleichung
Lineare Funktion
y = m(x-r)+s nennt man die Verschiebungsform der Geradengleichung [1] oder auch die Punktsteigungsform. Das m ist die Steigung der Geraden, das r ist die x-Koordinaten eines bekannten Punktes und das s ist y-Koordinaten desselben bekannten Punktes. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Umwandeln
Die Verschiebungsform y=m(x-r)+s ist formal identisch mit der sogenannten Punktsteigungsform y=m(x-X1)+Y1. Man kann das r genauso behandeln wie das X1 und das s wie das Y1. Die Umformung ist dann identisch mit der Umwandlung der => Punktsteigungsform in Normalform
Umwandeln
Die Verschiebungsform y=m(x-r)+s ist formal identisch mit der sogenannten Punktsteigungsform y=m(x-X1)+Y1. Man kann das r genauso behandeln wie das X1 und das s wie das Y1. Die Umformung ist dann identisch mit der Umwandlung der => Punktsteigungsform in Parameterform
Umwandeln
Die Verschiebungsform y=m(x-r)+s einer Geraden ist formal identisch mit der sogenannten Punktsteigungsform y=m(x-X1)+Y1. Um die eine Schreibweise in die andere umzuwandeln, genügt es, wenn das kleine r ersetzt durch X1 und das kleine s durch ein Y1. Siehe mehr dazu im Artikel zur Verschiebungsform der Geradengleichung => Ganzen Artikel lesen …
Umwandeln
Die Verschiebungsform y=m(x-r)+s ist formal identisch mit der sogenannten Punktsteigungsform y=m(x-X1)+Y1. Man kann das r genauso behandeln wie das X1 und das s wie das Y1. Die Umformung ist dann identisch mit der Umwandlung der => Punktsteigungsform in Zwei-Punkte-Form
Anschaulich
Als Verschiebungsstrom bezeichnet man jenen Anteil eines elektrischen Stroms, der zu seiner Entstehung keine freien Ladungsträger benötigt, die von Atom zu Atom oder von Molekül zu Molekül durch einen Leiter wandern können. Für das Auftreten eines Verschiebungsstroms genügt es, wenn sich positive und negative Ladungen innerhalb eines Materials auch auf nur kurze Distanzen zueinander verschieben können. Der Gedanke wird hier in seiner historischen Urversion von James Clerk Maxwell entwickelt. => Ganzen Artikel lesen …
Definition
In der Geometrie bezeichnet eine Verschiebung eine Ortsveränderung ohne Drehung. Solche Veränderungen kann man rechnerisch oft leicht mit Vektoren durchführen. Ein dazu genutzter Vektor heißt Verschiebungsvektor. => Ganzen Artikel lesen …
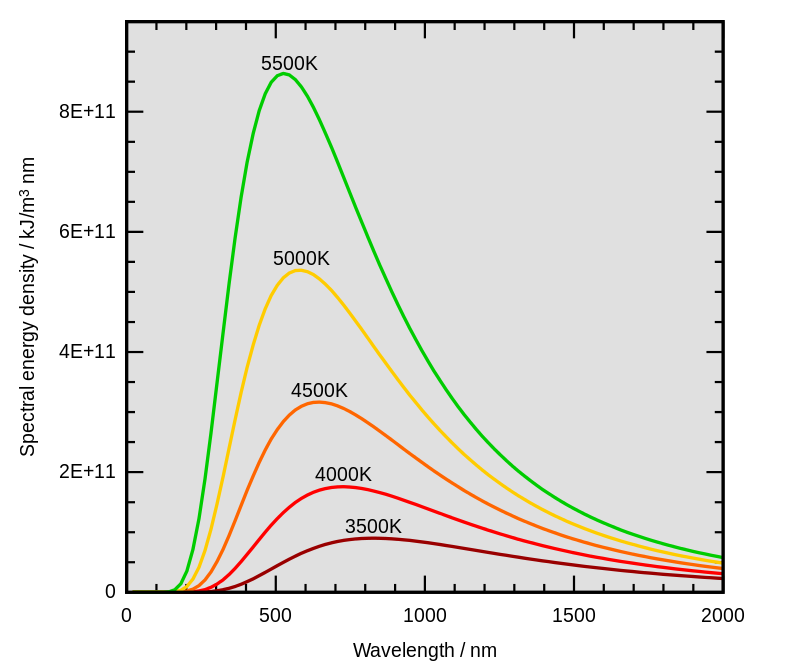Wiensches Verschiebungsgesetz
Physik
Je heißer, desto niedriger niedriger ist die Wellenlänge des Strahlungsmaximums: das nach Wilhelm Wien benannte Wiensche Verschiebungsgesetz besagt, dass die Wellenlänge, bei der ein Schwarzer Körper der absoluten Temperatur T die intensivste Strahlung abgibt, umgekehrt proportional zur Temperatur ist. Verdoppelt sich beispielsweise die Temperatur des Strahlers, so halbiert sich die Wellenlänge, bei der sein Strahlungsmaximum liegt. Allgemein gilt: "Das Licht eines glühenden undurchsichtigen Objektes hat ein charakteristisches Spektrum, das nur von seiner Tempemperatur abhängt - ein thermisches Spektrum [1, Seite 56]." Siehe auch => Schwarzer Strahler
