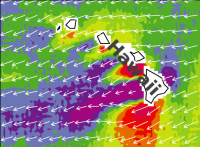
Vektorfeld
Mathematik
Angenommen auf einer Wetterkarte ist für jeden Punkt auf der Erdoberfläche die Windrichtung mit einem Pfeil eingetragen. Die Länge des Pfeiles steht dabei für die Stärke des Windes. Diese Darstellung wäre ein Vektorfeld: für jeden Punkt eines Raumes (auch einer Ebene) ist ein Vektor zugeordnet. => Ganzen Artikel lesen …
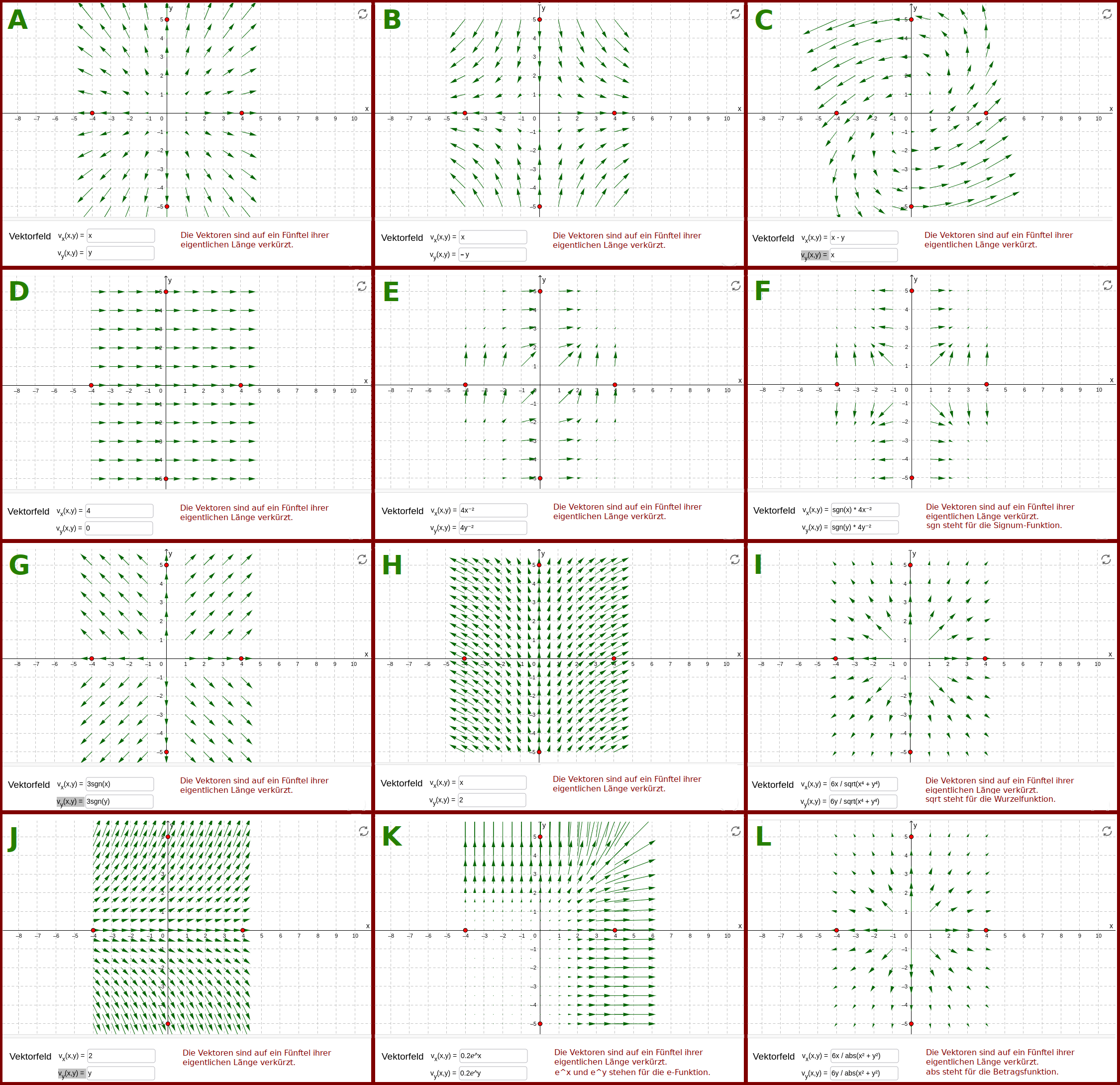Vektorfelder
Beispiele
Wie stark und in welche Richtung der Wind an verschiedenen Orten weht, kann man gut mit Pfeilen auf einer Landkarte darstellen. Solche Windfelder sind ein typisches Beispiel für sogenannte Vektorfelder. Die Vektoren sind dabei die Pfeile. Hier stehen einige weitere Beispiele dazu. => Ganzen Artikel lesen …
⊗☉↗⮅ Arten und Einteilung
Vektoren sind gedachte Pfeile in einem 2D-, 3D- oder höherem Koordinatensystem. Sie werden oft aus zwei oder drei Zahlen zusammengesetzt, etwa (4|3|5). => Ganzen Artikel lesen …
Vektorfuss
Ohne Spitze
Wird ein Vektor als Pfeil veranschaulicht, dann kann man das Ende des Vektors ohne die Pfeilspitze den Vektorfuß nennen. Auf ihn würde man den Pfeil stellen, wenn man ihn wie einen Speer in die Erde steckt. Das lange gerade Stück des Vektors ist dann der => Vektorschaft [auch Vektorachse]
Vektor
↗ Definition
Als Vektor bezeichnet man in der Mathematik oft einen Pfeil in einem 2D- oder 3D-Koordinatensystem. Er wird oft mit zwei, drei oder auch mehr Zahlen - den Vektorkoordinaten - geschrieben. Diese Zahlen sagen nichts darüber aus, wo ein Vektor in einem Koordinatensystem liegt. Die Zahlen sagen nur, wie lang der Vektor ist und in welche Richtung er zeigt. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Physik
Die Divergenz eines Vektorfeldes gibt für jeden Punkt des Feldes an, wie stark in seiner Umgebung die Vektoren auseinander streben. Die Divergenz selbst ist eine reine Zahl, also ein Skalar. Die Divergenz spielt unter anderem bei Strömungsfeldern und bei den Maxwell-Gleichungen der Elektrodynamik eine Rolle. => Ganzen Artikel lesen …
Physik
Ein Vektorfeld gilt in einem Bereich als quellfrei oder quellenfrei, wenn seine Feldlinien nirgends einen Anfang haben. Mathematisch ist das gleichbedeutend mit der Aussage, dass die Divergenz dort nirgend größer ist als 0. Es ist zudem frei von Senken, wenn die Divergenz nirgends kleiner ist als 0. Oft heißt quellenfrei aber etwas unpräzise, dass die Divergenz 0 sein soll. Eindeutiger ist es hier von einem divergenzfreien Feld zu sprechen. Siehe auch => Divergenz eines Vektorfeldes
… in der Physik und Vektoranalysis auch => quellenfreies Vektorfeld
Rotation eines Vektorfeldes
Physik
Die Rotation eines Vektorfeldes hängt anschaulich eng mit Wirbeln [1], Winkelgeschwindigkeiten [2] und der Rotation von Probekörpern um sich selbst in einem Strömungsfeld [3] von Flüssigkeiten [4] zusammen. Das ist hier mit Rechenbeispielen erklärt. => Ganzen Artikel lesen …
… siehe unter => Vektoranalysis
Physik
Als Zirkulation eines Vektorfeldes bezeichnet man das Integral entlang einer geschlossenen Linie, bei dem die Vektorkomponenten in tangentialer Richtung dieser Linie integriert, also gedanklich aufaddiert werden [1]. Siehe auch => Vektoranalysis
