Umkehrfunktion
x und y vertauscht
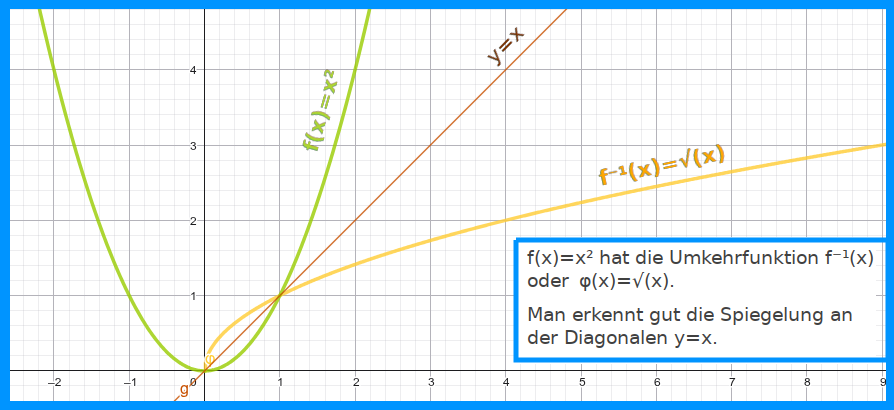
Die Variablen x und y vertauscht und dann nach x aufgelöst: so bildet man für eine gegebene Funktion f(x) die dazugehörige Umkehrfunktion f⁻¹ [2], auch inverse Funktion genannt. Diese Umwandlung ist aber nicht für alle Funktionstypen möglich. Hier stehen eine Anleitung sowie die anschauliche Bedeutung der Umkehrfunktion. => Ganzen Artikel lesen …
Beispiele
f(x) = x²+x ist eine typische Summenfunktion: kann man den Funktionsterm als Summe auffassen, kann man die ganze Funktion auch als Summenfunktion bezeichnen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Technischer Fachbegriff [Bergbau]
=> Ganzen Artikel lesen …
Umsatzfunktion
… heißt auch => Erlösfunktion
… Name für => f(x)=1:x
f(x)=1/x, auch geschrieben als f(x)=1:x nennt man auch die Kehrwertfunktion. Sie ist ein (einfacher) Sonderfall gebrochenrationaler Funktionen. Hier werden kurz einige Eigenschaften vorgestellt.
Fehlerfunktion
Wertetabelle
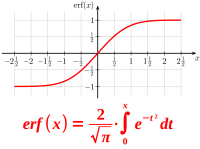
Die Fehlerfunktion oder auch Gaußsche Fehlerfunktion, oft geschrieben als erf(x) ist eine spezielle Sigmoidfunktion. Sie findet vor allem Anwendung in der Statistik. Ausgesprochen ist ihre Gleichung: f(x) = Integral von 0 bis x von 2 durch Wurzel aus pi mal dem Integral von e hoch minus-r-quadrat mal dr. Hier steht eine Wertetabelle. => Ganzen Artikel lesen …
… f⁻¹ finden, siehe unter => Umkehrfunktion bestimmen
Anleitung
y = 4x-12 hat als Umkehrfunktion y = 0,25x+3. Um die Umkehrfunktion f⁻¹(x) zu bilden, vertauscht man erst x und y. Dann löst man die so entstandene Gleichung nach y auf. Das Ergebnis ist die Umkehrfunktion. Das kleine y steht hier auch für f(x). Hier wird nur erklärt, wie man eine Umkehrfunktion bestimmt. => Ganzen Artikel lesen …
… Beispiele unter => keine Funktionen
… Beispiele unter => keine Funktionen
… Beispiele unter => keine Funktionen
