Tetraeder
Pyramidenart
Ein Tetraeder, auf Deutsch Vierflächner, ist ein Körper mit genau vier dreieckigen Begrenzungsflächen. Ein Tetraeder hat 4 Ecken und 6 Kanten. Man kann zwei Arten unterscheiden: die allgemeine Dreieckpyramide und den regelmäßigen Disphenoid. => Ganzen Artikel lesen …
Chemie
Ein Tetramer, z. B. Hämoglobin, ist ein Molekül aus vier (Tetra) Untereinheiten (mer) und damit ein spezielles => Polymer
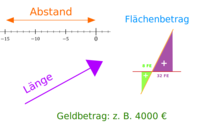
Beträge
Begriffsklärung
Beträge gibt es für Zahlen, Geldmengen, Vektoren, komplexe Zahlen, Integrale und andere mathematische Objekte. Die verschiedenen Bedeutungen werden hier kurz vorstellt. => Ganzen Artikel lesen …
Geometrie
Ein Körper mit sechs (vieleckigen) Flächen ist ein Hexaeder. Ist ein Hexaeder ganz regelmäßig, wird er auch platonischer Körper genannt. Ein Würfel ist ein typischer regelmäßiger Hexaeder. Siehe auch => Würfel
Wie viele Gramm, Kilogramm, Tonnen ein Tetraeder hat
Tetraedermasse = Tetraedervolumen * Dichte => Ganzen Artikel lesen …
Definition
⅓·a·√6 gibt die Höhe des Tetraeders, wenn seine Kanten alle dieselbe Länge a haben: ein Tetraeder im engeren Sinn ist eine Dreieckpyramide mit ausschließlich kongruenten gleichseitigen Seitenflächen. Die Höhe des Tetraeders ist definiert als die kürzeste Strecke von einer seiner Ecken zur gegenüberliegenden (dreieckigen) Seitenfläche. Das ist hire kurz erläutert. => Ganzen Artikel lesen …
… Dreieckpyramide mit beliebigen Flächen, mehr unter => Tetraeder
Allgemeines Tetraeder
… eine Dreieckpyramide mit beliebigen Flächen, mehr unter => Tetraeder
… Erklärung mit Berechnungstipp unter => Tetraedermasse
… Erklärung mit Berechnungstipp unter => Tetraedermasse
… alle Kanten gleich lang, siehe unter => reguläres Tetraeder
… Dreieckpyramide mit vier deckungsgleichen Flächen, mehr unter => Tetraeder
… Erklärung mit Berechnungstipp unter => Tetraedermasse
… Dreieckpyramide mit beliebigen Flächen, mehr unter => Tetraeder
… ein Tetraeder mit vier deckungsgleichen Flächen => Tetraeder
Formel
Ein Tetraeder ist ein Körper mit nur dreieckigen Seitenflächen. Ein Tetraeder hat genau vier Ecken und vier Seitenflächen sowie sechs Kanten. Alle sechs Kanten sind gleich lang, ihre Länge kürzt man zum Beispiel ab mit einem kleinen a. => Ganzen Artikel lesen …
Tetraederformeln
Formeln rund um ein Tetraeder
- => Tetraedervolumen
… Erklärung mit Berechnungstipp unter => Tetraedermasse
Formel für die Höhe k eines Tetraeders
Ein Tetraeder im engeren Sinn ist eine Dreieckpyramide mit ausschließlich kongruenten gleichseitigen Seitenflächen. Die Höhe des Tetraeders ist definiert als die kürzeste Strecke von einer seiner Ecken zur gegenüberliegenden (dreieckigen) Seitenfläche. => Ganzen Artikel lesen …
Tetraederoberfläche
Formel
√3 mal a gibt die Tetraederoberfläche: ein Tetraeder ist eine Dreieckpyramide bei der alle sechs Kanten dieselbe Länge haben, die Länge kürzt man oft ab mit einem kleinen a. Aus dieser Kantenlänge kann man dann immer direkt den Inhalt der Oberfläche berechnen. Zur Oberfläche zählen alle vier Seitenflächen, auch der Boden, des Tetraeders. => Ganzen Artikel lesen …
… Erklärung mit Berechnungstipp unter => Tetraedermasse
Tetraedervolumen
Volumen V für ein reguläres Tetraeder
Als Tetraeder im engeren Sinn bezeichnet man eine Dreieckpyramide mit ausschließlich gleichseitigen und kongruenten Seitenflächen (alle gleich groß, alle gleiche Form). Solche Tetraeder nennt man regulär. Die folgende Formel gilt nur für reguläre Tetraeder: => Ganzen Artikel lesen …
Beispiele
Ein Tetraeder ist eine Dreieckpyride mit nur gleich langen Seiten. Das Volumen berechnet man über die Formel a·a·a:12 mal (Wurzel aus 2), kurz: a³·√2. Hier stehen einige Beispielhafte Rechenergebnisse für verschieden Werte der Kantenlänge a. => Ganzen Artikel lesen …
