 Tangentengleichung
Tangentengleichung
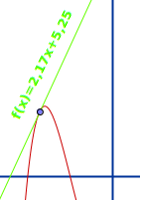
Geradengleichung mit gleicher Steigung wie f(x)
Definition: Eine Tangente t(x) ist immer eine Gerade, die einen Punkt mit einem anderen Graphen f(x) gemeinsam hat. Die Tangente und der Graph haben an diesem Punkt dieselbe Steigung. Es wird erklärt, was genau eine Tangente im Zusammenhang mit Graphen ist und wie man ihre Gleichung aufstellt. => Ganzen Artikel lesen …
Ausführliche Beispiele
Tangenten an Grapen von Funktionsgleichungen: hier stehen Beispiele für eine Parabel und eine Hyperbel. => Ganzen Artikel lesen …
… siehe unter => Raketenformel
 Tangentensteigung
Tangentensteigung
Definition
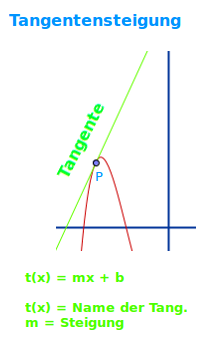
Die Tangente im Sinne der Analysis (Funktionsgraphen) ist immer eine Gerade. Sie schneidet oder berührt den Graphen an einem Punkt so, dass sie dort dieseelbe Steigung hat wie der Graph. Die Tangentensteigung ist dann auch die Steigung des Graphen an diesem Punkt. => Ganzen Artikel lesen …
… Anleitung unter => Tangentengleichung aufstellen
… Tipps mit Aufgaben, siehe => Wendetangenten bestimmen
… wie es geht steht unter => Tangentengleichung aufstellen
… wie es geht steht unter => Tangentengleichung aufstellen
… Tipps mit Aufgaben, siehe => Tangentengleichung aufstellen
… siehe unter => Tangentengleichung aufstellen
=> Ganzen Artikel lesen …
 Tangentengleichung aufstellen
Tangentengleichung aufstellen
Anleitung
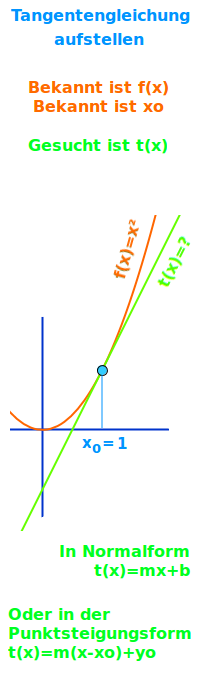
t(x) = mx+b - es wird erklärt, wie man für einen gegebenen Punkt auf einem gegebenen Funktionsgraphen f(x) eine passende Tangentengleichung t(x) bestimmt. Es werden zwei verschiedene (aber ähnliche) Methoden vorgestellt, die immer auch dasselbe Ergebnis liefern. Am Ende stehen auch Aufgaben mit Lösungen. => Ganzen Artikel lesen …
… Tipps mit Aufgaben, siehe => Tangentengleichung aufstellen
… t(x) = ? => Tangentengleichung aufstellen
… es gibt mehrere => Extrempunkttangenten
… Definition unter => Hochpunkttangente
… Definition unter => Tiefpunkttangente
 Tangentengleichung über Normalform
Tangentengleichung über Normalform
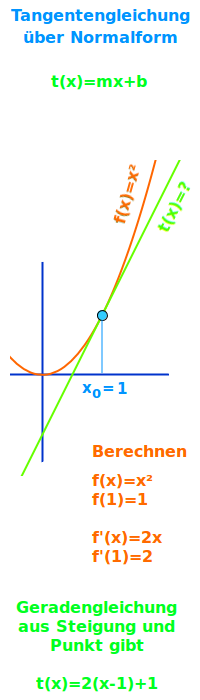
Wie man t(x)=mx+b für eine Tangente findet
Gegeben ist eine Funktionsgleichung f(x) und der x-Wert eines Punktes auf dem Graphen. Daraus kann man die Gleichung y=mx+b der Tangente an dem Punkt bestimmen. Das wird hier Schritt für Schritt erklärt. => Ganzen Artikel lesen …
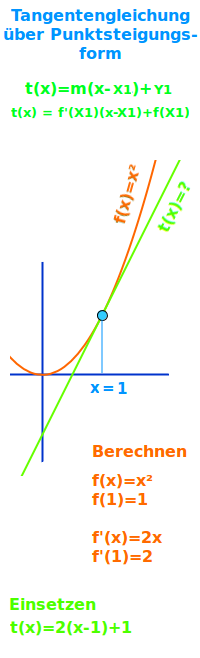 Tangentengleichung über Punktsteigungsform
Tangentengleichung über Punktsteigungsform
Anleitung
Gegeben ist eine Funktionsgleichung f(x) und der x-Wert eines Punktes (X1|Y1) auf dem Graphen. Daraus kann man die Gleichung t(x) in der Form t(x) = m·(x-X1)+Y1 der Tangente an dem Punkt (X1|X2) bestimmen. Dieser Rechenweg ist schnell ohne große Fehlermöglichkeiten. Das wird hier Schritt für Schritt erklärt. => Ganzen Artikel lesen …
… siehe unter => Tangentengleichung aufstellen
… siehe unter => Tangentengleichung aufstellen
… wie es geht steht unter => Tangentengleichung aufstellen
… Tipps mit Aufgaben, siehe => Tangentengleichung aufstellen
… Tipps mit Aufgaben, siehe => Wendetangenten bestimmen
… Tipps mit Aufgaben, siehe => Wendetangenten bestimmen
… Tipps mit Aufgaben, siehe => Wendetangenten bestimmen
… Tangenten sind Geraden, siehe unter => y-Achsenabschnitt von Geraden bestimmen
… Tangenten sind Geraden, siehe unter => y-Achsenabschnitt von Geraden bestimmen

