Senkrechte Steigung
Mathematisch
Eine senkrechte Steigung ist als Steigungswinkel 90°. Als Steigunger einer linearen Funktion ist senkrecht nicht definiert. Und ein Beispiel aus der Wirklichkeit ist eine Steilwand: Diese Beispiele und auch, was eine senkrechte Gerade in einem xy-Koordinatensystem ist, wird hier kurz erklärt. => Ganzen Artikel lesen …
Senkrechte
Etwas mit 90°-Winkel
Ein Sendemast ragt zum Beispiel als Senkrechte in den Himmel: eine Gerade, Strecke oder Ebene kann eine Senkrechte zu etwas anderem sein. Das heißt, es gibt einen rechten Winkel (90°). Verschiedene Fälle, die dabei auftreten können sind ausführlicher erklärt in dem Artikel => Orthogonale
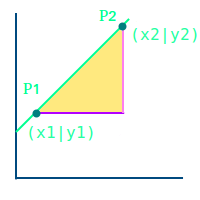Steigung
Übersicht
Steigung an sich sagt, wie steil etwas nach oben oder unten geht. In der Mathematik berechnet man die Steigung meist über ein Steigungsdreieck. Die Steigung ergibt sich dann aus der Höhe dieses Dreiecks geteilt durch seine Breite. => Ganzen Artikel lesen …
Waagrechte Steigung
wäre bei einem Funktionsgraphen die Steigung 0.
Sekantensteigung
Definition
Steigung der Geraden durch P und Q: in der Funktionsgleichung y=mx+b ist die Sekantensteigung die Zahl, die an der Stelle des Buchstaben m steht. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
… kann mehrere Dinge bedeuten, siehe unter => senkrechter Strich
In der Mathematik
|4| sind Betragsstriche. Bei {x| x<3} liest man den Strich als „derart dass“. Auf einem Blatt Papier nennt man Striche senkrecht, wenn sie von oben nach unten gezeichnet sind. Hier werden verschiedene Bedeutungen aus der Mathematik kurz erklärt. => Ganzen Artikel lesen …
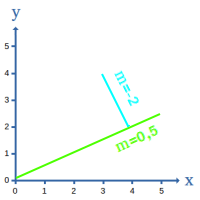Zueinander senkrechte Steigungen berechnen
Rechenbeispiel
xy-Koordinatensystem. Man hat eine Gerade und sucht die Steigung einer dazu senkrechten Geraden. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
