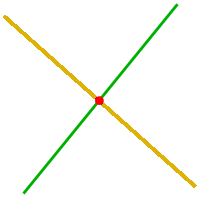
Schnittpunkt

Definition

Ein Schnittpunkt ist ein gemeinsamer Punkt von zwei oder mehr Objekten. Ein Schnittpunkt muss also gleichzeitig zu mindestens zwei Objekten gehören. Objekte können sein: Mengen, Körper, Flächen, Linien, Geraden, Punktemengen etc. => Ganzen Artikel lesen …

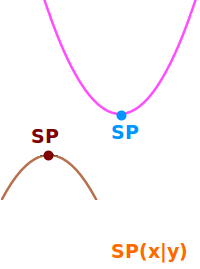Scheitelpunkt

Mathematik

Bei Funktionsgraphen ist ein Scheitelpunkt (SP) der höchste oder tiefste Punkt einer Parabel. Neben dieser Bedeutung gibt es aber auch noch weitere. => Ganzen Artikel lesen …

4: Scheitelpunkte

… von Parabeln, siehe unter => Scheitelpunkte von Parabeln

6: 2D-Schnittpunkte von Geraden bestimmen

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

11: Ganzrationale Parabel y-Achse Schnittpunkt

… siehe unter => y-Achsenabschnitt von ganzrationalen Funktionen

12: Ganzrationale Parabel y-Achse Schnittpunkt bestimmen

… siehe unter => y-Achsenabschnitt von ganzrationalen Funktionen bestimmen

13: Gerade Parabel Schnittpunkt

… Anleitung und Aufgaben unter => Schnittpunkte von Parabeln mit Geraden berechnen => qck

14: Gerade Schnittpunkt

… siehe unter => Schnittpunkte von Geraden

15: Gerade y-Achse Schnittpunkt

… ist erklärt unter => y-Achsenabschnitt von Geraden

16: Gerade y-Achse Schnittpunkt bestimmen

… ist erklärt unter => y-Achsenabschnitt von Geraden bestimmen

17: Geraden Parabeln Schnittpunkte

… Anleitung und Aufgaben unter => Schnittpunkte von Parabeln mit Geraden berechnen => qck

18: Geraden und Parabeln Schnittpunkte

… Anleitung und Aufgaben unter => Schnittpunkte von Parabeln mit Geraden berechnen => qck

19: Geradenschnittpunkt

… kann mehrere Dinge bedeuten, siehe unter => Geradenschnittpunkte

20: Geradenschnittpunkt graphisch bestimmen

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

21: Geradenschnittpunkte

… Übersicht unter => Schnittpunkte von Geraden

22: Geradenschnittpunkte graphisch bestimmen

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

23: Geradenschnittpunkte über Vektoren

… siehe unter => Geradenschnittpunkte über Vektorrechnung

25: Gradenschnittpunkt graphisch bestimmen

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

26: Gradenschnittpunkte graphisch bestimmen

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

27: Graphische Schnittpunktbestimmung von Geraden

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

29: Kubische Funktionen Schnittpunkte mit x-Achse bestimmen

… mehrere Methoden unter => Nullstellen von kubischen Funktionen bestimmen

30: Kubische Parabel y-Achse Schnittpunkt

… siehe unter => y-Achsenabschnitt von kubischen Funktionen

31: Lineare Funktion Schnittpunktbestimmung

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

32: Lineare Funktion Schnittpunkte bestimmen

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

33: Lineare Funktionen Schnittpunkt bestimmen

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

34: Lineare Funktionen Schnittpunkte bestimmung

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

35: Lineare Funktionen Schnittpunkte mit x-Achse bestimmen

… mehrere Methoden unter => Nullstellen von Geraden bestimmen