Punktsteigungsform der Geradengleichung
Kann man direkt aus Punkt und Steigung erstellen
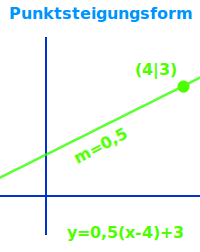
y = m(x-X1)+Y1 oder y-Y1 = m(x-X1) nennt man die Punktsteigungsform oder auch die Verschiebungsform. Man kann sie ohne Rechnung direkt aus einem gegebenen Punkt und der bekannten Steigung erstellen. Man muss dazu nicht rechnen. Das ist ihr Vorteil. => Ganzen Artikel lesen …
y=m(x-X1)+Y1 oder y-Y1=m(x-X1)
Man kennt einen Punkt einer Geraden und die Steigung. Daraus kann man ohne Rechnung eine Funktionsgleichung erstellen über die => Punktsteigungsform der Geradengleichung
Geradengleichung
Definition
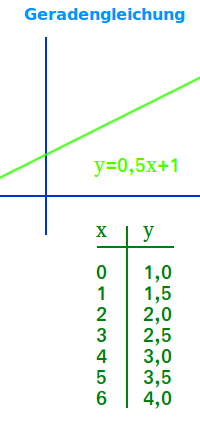
y = 2x+1 ist eine typische Geradengleichung. Sie hat zwei Unbekannte, oft x und y genannt. Ihr Graph ist eine Gerade, daher der Name. Hier steht mehr zur Definition und zur Lösung solcher linearen Gleichungen. => Ganzen Artikel lesen …
… als lineare Funktion => Punktsteigungsform der Geradengleichung
Lineare Funktion
y = m(x-r)+s nennt man die Verschiebungsform der Geradengleichung [1] oder auch die Punktsteigungsform. Das m ist die Steigung der Geraden, das r ist die x-Koordinaten eines bekannten Punktes und das s ist y-Koordinaten desselben bekannten Punktes. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Analysis
C = Ax + By nennt man auch die allgemeine Form einer Geradengleichung oder einer linearen Funktion. Das y entspricht dabei auch dem Funktionsterm f(x). Stellt man nach y um, erhält man y = -(A/B)·x + C/B. Diese Form ist eher ungebräuchlich im Sinne einer Funktionsgleichung. Sie ist aber eine typische Form für eine => lineare Gleichung mit zwei Unbekannten
Schreibweisen
Eine Geradengleichung in einem xy-Koordinatensystem kann man in verschiedenen Formen darstellen. Die Zwei-Punkte-Form ist eine von ihnen. Ihr großer Vorteil ist: mnan kann sie sofort hinschreiben, wenn man zwei Punkte der Geraden kennt. Neben der Variante im xy-Koordinatensystem (2D) gibt es auch noch eine Geradengleichung für zwei Punkte in einem dreidimensionalen xyz-Koordinatensystem (3D). Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… gut, wenn man P und Q kennt => Zwei-Punkte-Form der Geradengleichung
