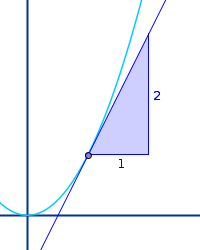
Parabelsteigung
An einem Punkt
Eine Parabel als Funktionsgraph hat an jedem Punkt eine andere Steigung. Am Scheitelpunkt ist die Steigung immer gleich 0. Links und rechts nach außen auf den Parabelästen wird der Graph dann immer steiler: der Betrag der Steigung nimmt zu. Das ist hier erklärt. => Ganzen Artikel lesen …
… ist an jedem Punkt anders, mehr unter => Parabelsteigung
Längung entlang der x- und y-Achse
Streckung heißt: in die Länge gezogen: eine gestreckte Parabel wirkt dünner als die Ausgangsparabel. Man unterscheidet eine Streckung in x- und in y-Richtung. Eine Anleitung steht unter => Parabel strecken
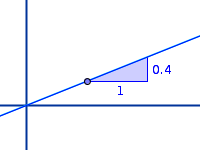Geradensteigung
m
Zahl für die Steilheit: die Geradensteigung, oft als m abgekürzt, ist dasselbe wie die Steigung einer linearen Funktion. Es wird erklärt, was genau das bedeutet und wie man die Geradensteigung bestimmen kann (es gibt verschiedene Methoden). => Ganzen Artikel lesen …
… Funktionsterm mal Streckungsfaktor -1 bis 1, mehr unter => Parabeln stauchen
Über f'(x)
Eine Parabel als Graph einer quadratischen Funktion hat an jeder Stelle eine andere Steigung. Es gibt keine zwei Punkte, die dieselbe Steigung haben. Die Steigung für jeden einzelnen Punkt einer Parabel kann man leicht mit Hilfe der ersten Ableitung f'(x) berechnen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Bestimmung
Eine Parabel hat an jedem Punkt eine andere Steigung. Setzt man die x-Koordinate eines Punktes in die erste Ableitung der Funktionsgleichung ein, erhält man als Ergebnis direkt die Steigung der Parabel an diesem Punkt. Das ist hier am Beispiel von f(x) = 4x²-2x+8 kurz vorgerechnet. => Ganzen Artikel lesen …
