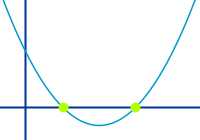
Nullstellen von quadratischen Funktionen bestimmen
Übersicht
Nullstellen von quadratischen Funktionen, das heißt auch die Nullstellen der dazugehörigen Parabeln, kann man mit verschiedenen Methoden bestimmen. Ein guter Standard ist die pq-Formel. Die pq-Formel funktioniert immer. Daneben gibt es aber auch noch einige Alternativen, die manchmal schneller zum Ziel führen. => Ganzen Artikel lesen …
Nullstellen
Beispiele
Nullstellen sind x-Werte auf der x-Achse, bei denen ein Funktionsgraph die x-Achse schneidet. Hier sind Beispiele für z. B. Geraden, Parabeln, Kubische, ganzrationale und einige andere Funktionstypen. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
Übersicht
Funktionen wie f(x)=4x+5 oder f(x)=x²-1 werden nach verschiedenen Kriterien klassifiziert. Einige der wichtigsten werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Bestimmen
(Irgendwie) herausfinden
Bestimmen heißt: etwas herausfinden, wobei der genaue Weg dazu aber offen gelassen wird. Man kann etwas über eine Berechnung, über Schätzen, über Recherchieren oder sonstwie bestimmen. => Ganzen Artikel lesen …
Übersicht
Substitution, Nullprodukt, Faktorisieren, planvolles Probieren sowie auch einige exotische Verfahren: für biquadratische Funktionen wie zum Beispiel f(x) = x⁴ + x² - 12 gibt es verschiedene Verfahren zur Bestimmung der Nullsetzen. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
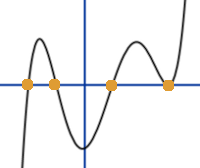Nullstellen von quartischen Funktionen bestimmen
Übersicht
f(x)=x⁴-81: quartisch nennt man eine ganzrationale Funktion bei der der höchste Exponent von x die Zahl 4 ist. Dafür gibt es verschiedene Lösungsverfahren für Nullstellen: Probieren, Nullprodukt und Faktorisieren. Diese sind hier mit Beispielen vorgestellt. => Ganzen Artikel lesen …
… siehe => Nullstellen von biquadratischen Funktionen bestimmen
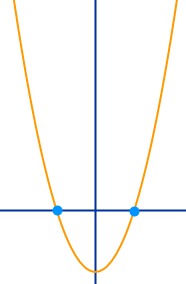Nullstellen von reinquadratischen Funktionen bestimmen
Übersicht
f(x) = ax² + c ist der Bauplan einer reinquadratischen Funktion. Es gibt immer ein Glied mit x². Es darf noch ein Glied ohne x geben, das sogenannte absolute Glied. Was nicht vorkommen darf sind sogenannte lineare Glieder, also ein Glied mit x ohne hoch zwei. Solche Gleichungen lassen sich immer leicht über Umformen lösen. Da ist hier erklärt. => Ganzen Artikel lesen …
