Nullstellen über Probieren
Schnelles Verfahren
Probieren meint hier ein intelligentes und kontrolliertes Raten, bei dem schnell erste brauchbare Ergebnisse erzielt werden können. => Ganzen Artikel lesen …
Nullstellen
Beispiele
Nullstellen sind x-Werte auf der x-Achse, bei denen ein Funktionsgraph die x-Achse schneidet. Hier sind Beispiele für z. B. Geraden, Parabeln, Kubische, ganzrationale und einige andere Funktionstypen. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Ist oft schnell
Mit ratendem oder systematischen Probieren kann man viele Gleichungen oft schnell und einfach lösen. Probierverfahren werden in der Mathematik sehr oft eingesetzt. Sie gelten oft als effizient. Dazu steht hier ein Beispiel. => Ganzen Artikel lesen …
=> Ganzen Artikel lesen …
Verfahren
Faktorisieren heißt einen Term in eine Malkette, auch Produkt genannt, umzuformen. Aus Malketten kann man Nullstellen von Funktionen oft direkt ohne weiteres Rechnen ablesen. Dazu sind hier einige häufige Verfahren vorgestellt. => Ganzen Artikel lesen …
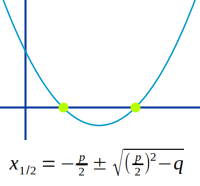Nullstellen über pq-Formel
-p/2 ± √[(p/2)²-q]
f(x) = x²-6x+8 ist eine quadratische Funktion. Das p ist hier die Zahl -6 und q ist 8. In die Formel eingesetzt erhält man die x-Werte, bei denen die Parabel die x-Achse schneidet, also die Nullstellen. Im Beispiel sind es x=2 und x=4. Das Lösungsverfahren wird hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Methode
f(x) = 2x-8 ⭢ 0 = 2x-8 ⭢ umformen ⭢ x = 4 ✔: die Nullstellen von linearen (Geraden), quadratischen oder kubische Funktionen kann man oft am schnellsten durch einfaches Umformen bestimmen. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
