Matrizen
… Arten von Matrizen; Themenübersicht unter => Matrizenrechnung
Verschiedene Bedeutungen im Sinne von Gußform
Druckereiwesen: eine Form zum Guss von Einzelbuchstaben => Ganzen Artikel lesen …
Erlaubte Mehrzahl von Matrix. Gebräuchlich ist „Matrizen“.
… erlaubte aber ungewöhnliche Mehrzahl von Matrix, üblich => Matrizen
… Matrizen ist die Mehrzahl einer => Matrix
… Rechenregel unter => Matrix plus Matrix
… Rechenregel unter => Matrix plus Matrix
Stabile Verteilung
Stochastische Prozesse haben oft eine sogenannte stabile Verteilung. Kennt man die stochastische Matrix des Prozesses kann man darüber beurteilen, ob der Prozess irgendwann eine stabile Verteilung annimmt, die Verteilung sich also nicht mehr verändert. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
Beispiele
Eine reguläre (Determinante ist nicht 0), quadratische Matrix (Zeilenzahl = Spaltenzahl) kann immer in eine invertierte Matrix umgewandelt werden. Dazu gibt es verschiedene Rechenverfahren, die eher aufwändig sind. Eine Matriz mal ihrer Inversen ergibt immer die Einheitsmatrix. Hier stehen Beispiele. => Ganzen Artikel lesen …
… Anleitung unter => inverse Matrix berechnen
… Anleitung unter => inverse Matrix berechnen
Übersicht
Matrix durch Matrix oder Matrix durch Zahl: das inverse Element der Division mit Matrizen kann mehrere Dinge meinen, je nach Divisionsart. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
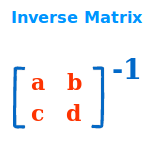Inverses Element der Matrizenmultiplikation
Übersicht
Matrix mal Matrix, Matrix mal Zahl oder Zahl mal Matrix: für diese Fälle ist hier das inverse Element der Multiplikation kurz erklärt. => Ganzen Artikel lesen …
Zahlenwerte
Matrizen sind tabellenartigen Strukturen von Zahlen. Die reinen Zahlen an sich heißen Koeffizienten. Mehr zur Defininition unter => Koeffizient einer Matrix
… jede Zahl in einer Matrix, mehr unter => Koeffizient einer Matrix
… Rechenregel unter => Matrix plus Matrix
Definition
Matrix durch Zahl ist definiert und kann gerechnet werden. Aber eine Zahl durch eine Matrix oder auch eine Matrix durch eine Matrix dividieren ist nicht definiert. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… Anleitung unter => inverse Matrix berechnen
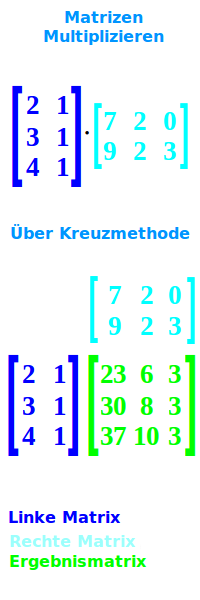Matrizen multiplizieren
Übersicht
Matrix mal Zahl ist dasselbe wie Zahl mal Matrix. Völlig anders gerechnet wird hingegen Matrix mal Matrix. Alle drei Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… Rechenregel unter => Matrix plus Matrix
… Rechenregel unter => Matrix plus Matrix
Begriffsklärung
Eine Matrix ist ein mathematisches Objekt aus tabellenartig angeordneten Zahlen. Man kann etwas von einer solchen Matrix subtrahieren (abziehen) oder eine Matrix von etwas subtrahieren. Hier steht eine kurze Übersicht zu verschiedenen Weisen zum Subtrahieren von Matrizen. => Ganzen Artikel lesen …
… Rechenregel unter => Matrix plus Matrix
… siehe unter => Matrizen dividieren
… um eine Matrix zu invertieren, steht unter => Gauß-Jordan-Verfahren
… um eine Matrix zu invertieren, steht unter => Gauß-Jordan-Verfahren
… jede Zahl in einer Matrix, mehr unter => Koeffizient einer Matrix
… jede Zahl in einer Matrix, mehr unter => Koeffizient einer Matrix
Eigenschaften
Eine Matrix mal einer anderen Matrix: das nennt man eine Matrizenmultiplikation. Es gelten dafür besondere Rechenregeln, die hier kurz vorgestellt sind. Am Ende ist auch erklärt, wie man Matrizen multipliziert. => Ganzen Artikel lesen …
… Es gibt mehrere Methoden, siehe unter => Rang einer Matrix berechnen
… es gibt mehrere Methoden, siehe unter => Rang einer Matrix berechnen
Was ist der Rang?
Dazu gibt es verschiedene Methoden. Sie werden kurz vorgestellt unter => Rang einer Matrix berechnen
… es gibt mehrere Methoden, siehe unter => Rang einer Matrix berechnen
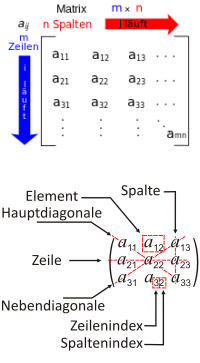Matrizenrechnung
Fachworte
Hier stehen Rechenwarten und Fachworte rund um Matrizen. Matrizen sind in Tabellen angeordnete Zahlen. Für Matrizen gibt es besondere Rechenregeln. Typische Anwendungsgebiete für Matrizen sind stochastische Prozesse sowie Produktionsprozesse. => Ganzen Artikel lesen …
Fachwörter
Hier stehen Fachwörter zur Mathematik der Matrizen alphabetisch sortiert von A bis Z. Am Ende der Liste stehen auch weiterführende Verweise. => Ganzen Artikel lesen …
