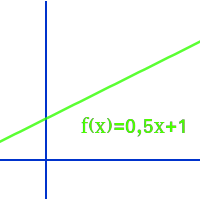
Lineare Funktion

y=mx+b

Jede Funktion, deren Funktionsgleichung man in der Form f(x)=mx+b schreiben kann heißt linear. Der Graph einer linearen Funktion ist immer einer Gerade (aber nicht jede Gerade gehört zu einer linearen Funktion). Auf dieser Seite stehen wichtige Fachworte zu linearen Funktionen. => Ganzen Artikel lesen …

Funktion

f(x)

f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …

Lineare Funktionen

Beispiele

Linear nennt man jede Funktion, deren Gleichung man in die Form f(x)=ax+b oder f(x)=mx+b bringen kann. Der Graph einer linearen Funktion ist immer eine Gerade. Die Funktionsgleichung einer linearen Funktion ist immer eine Geradengleichung. Es folgen einige Arten und Beispiele. Eine Übersicht zum gesamten Thema steht auf => lineare Funktion

4: Innere Funktion

… in der Analysis, siehe unter => verkettete Funktion

5: Linienfunktion

… wie f(x)=2x+4, mehr unter => Lineare Funktion

6: Inverse Funktion

… von y=0,5·x+8 ist y=2x-16, heißt auch => Umkehrfunktion

7: Aus Texten lineare Funktion erstellen

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text

8: Aus Texten lineare Funktionen aufstellen

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text

9: Diskussion lineare Funktionen

… siehe unter => Lineare Funktionen Diskussion

10: Echolotformel als lineare Funktion

… 700 mal Laufzeit in Sekunden = ungefähre Wassertiefe in Metern, mehr => Echolotformel

12: Graph für lineare Funktion zeichnen

… zum Beispiel für y=2x+4, siehe unter => Graph aus Geradengleichung

16: Lineare Funktion ablesen

… z. B. y=4x+8 aus Graph bestimmen => Geradengleichung aus Graph

17: Lineare Funktion Achse Abschnitt bestimmen

… siehe unter => y-Achsenabschnitt von Geraden bestimmen

19: Lineare Funktion aufleiten

… f(x) = ax+b wird zu F(x) = ½·ax²+bx, mehr unter => Aufleitungsregeln

21: Lineare Funktion aufstellen aus Graph

… wie z. b. f(x)=2x+5, siehe unter => Geradengleichung aus Graph

22: Lineare Funktion aufstellen aus Texten

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text

23: Lineare Funktion aus Graph

… z. B. y=3x+4 oder f(x)=2x-1, siehe unter => Geradengleichung aus Graph

24: Lineare Funktion aus Graph ablesen

… z. B. y=4x+8 aus Graph bestimmen => Geradengleichung aus Graph

25: Lineare Funktion aus Graph bestimmen

… z. B. y=4x+8 aus Graph bestimmen => Geradengleichung aus Graph

26: Lineare Funktion aus Graph über Punkt und Punkt

… siehe unter => Geradengleichung aus Graph über zwei Punkte

27: Lineare Funktion aus Graph über Punkt und Steigung

… siehe unter => Geradengleichung aus Graph über Steigung und Punkt

28: Lineare Funktion aus Graph über Steigung und Punkt

… siehe unter => Geradengleichung aus Graph über Steigung und Punkt

29: Lineare Funktion aus Graph über Steigung und y-Achsenabschnitt

… Schritt-für-Schritt Anleitung unter => Geradengleichung aus Graph über Steigung und y-Achsenabschnitt

30: Lineare Funktion aus Graph über y-Achsenabschnitt und Steigung

… Schritt-für-Schritt Anleitung unter => Geradengleichung aus Graph über Steigung und y-Achsenabschnitt

31: Lineare Funktion aus Graph über zwei Punkte

… siehe unter => Geradengleichung aus Graph über zwei Punkte

32: Lineare Funktion aus Texten

… Erklärung und Aufgaben unter => Geradengleichung aus Text

33: Lineare Funktion aus Versuch

… Schülerversuche zu linearen Funktion => Geradengleichung aus Versuch

34: Lineare Funktion aus y-Achsenabschnitt und Punkt

… wie die Geradengleichung y=mx+b daraus aufstellt => Geradengleichung aus y-Achsenabschnitt und Punkt

35: Lineare Funktion aus zwei Punkten

… Anleitung unter => Geradengleichung aus zwei Punkten