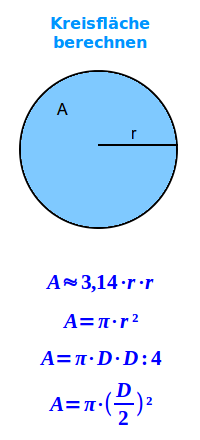
Kreisfläche berechnen
A = π·r²
Pi (etwa 3,14) mal den Radius mit sich selbst malgenommen. Beispiel: für den Radius r = 2 Meter rechnet man: 3,14·2·2 = 12,56 m². Das ist die einfachste Formel. Daneben gibt es noch weitere. Diese werden hier kurz vorgestellt. => Ganzen Artikel lesen …
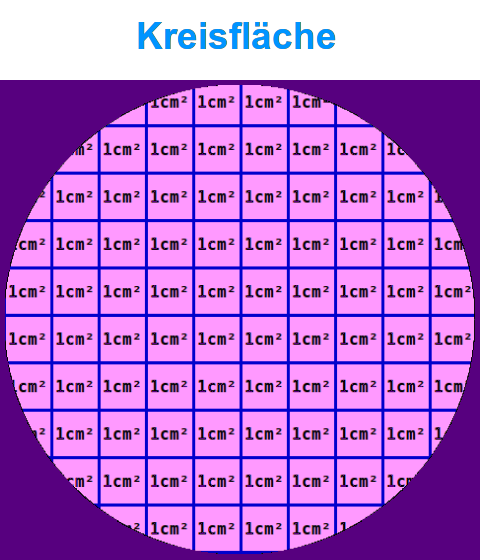Kreisfläche
⬤ A=πr²
Die Kreisfläche ist die Fläche innerhalb des äußersten Randes eines Kreises. Oft steht Kreifsläche auch kurz für den Inhalt dieser Fläche, etwa in cm². => Ganzen Artikel lesen …
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
… Formeln unter => Kreisflächenformeln
A = pi mal r²
pi ist immer etwa die Zahl 3,14. Neben dieser Formel gibt es noch verschiedene andere. Einen Einstieg in das Thema bietet die Seite => Kreisfläche berechnen
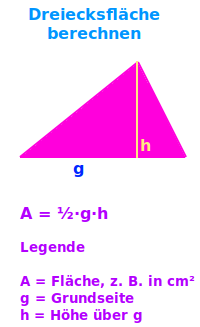Dreiecksfläche berechnen
Anleitung
A = ½·g·h - das ist die einfachste Formel, um eine Dreiecksfläche zu berechnen. Diese Formel funktioniert mit jedem Dreieck. Es gibt auch andere Formeln, diese passen aber oft nur auf bestimmten Dreiecksarten. Unten steht eine Übersicht zu allen Formeln. => Ganzen Artikel lesen …
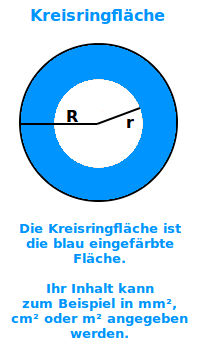Kreisringfläche berechnen
A = π·R²-π·r²
Ein Kreisring ist das, was übrig bleibt, wenn man von einer Kreisscheibe in der Mitte einen kleineren Kreis herausschneidet. Das Wort Kreisringfläche meint oft auch den Flächeninhalt dieses Kreises. Man kann ihn zum Beispiel angeben in cm² oder m². In diesem Artikel ist beschrieben, wie man diese Kreisringfläche A berechnet. => Ganzen Artikel lesen …
Formel
½·pi·r·r oder kurz geschrieben als ½·π·r² gibt den Inhalt einer Halbkreisfläche. Das Ergebnis kann man zum Beispiel in Quadratzentimetern (cm²) oder Quadratmetern (m²) angeben. Die Halbkreisfläche ist die Hälfte einer ganzen => Kreisfläche
