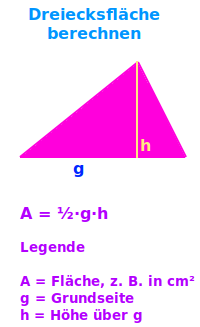Basiswissen

Mögliche Grundformeln

• A = 0,5·g·h
  

• A = ½·g·h
  

• A = g·h:2
  

Legende

• A = Flächeninhalt des Dreiecks, z. B. in cm²
  

• g = Grundseite (irgendeine der drei Seiten), z. B. in cm
  

• h = Höhe auf der ausgewählten Grundseite g, z. B. in cm
  

1. Schritt: Grundlinie wählen

• Man kann jedes Seite eines Dreiecks als Grundlinie wählen.
  

• Die übliche Bezeichnung für die Grundlinie ist das kleine g.
  

• Am einfachsten ist es, wenn man die längste der drei Seiten wählt.
  

• Miss ihre Länge, z. B. in cm.
  

• Das ist das g für die Formel.
  

• Siehe auch Dreiecksgrundlinie ↗
  

2. Schritt: Höhe bestimmen

• Wähle die Ecke gegenüber der Grundlinie g aus. Sie heißt hier: G
  

• Nimm ein Geodreieck. Die längste Seite des Geodreiecks heißt "Basis".
  

• Lege das Geodreieck flach auf das Dreieck. Drehe es so, dass die Basis durch die Ecke G geht.
  

• Drehe dann das Geodreieck so, dass die Basis einen 90°-Winkel mit der Grundlinie g bildet.
  

• Verbinde dann die Grundlinie g des Dreiecks mit der gegenüberliegenden Ecke G des Dreiecks.
  

• Diese Verbindungsstrecke ist dann die Höhe h des Dreiecks.
  

• Miss ihre Länge, z. B. in cm.
  

• Das ist dann das h für die Formel.
  

• Siehe auch Dreieckshöhe ↗
  

3. Schritt: Flächeninhalt

• Rechne g mal h und teile das Ergebnis durch 2.
  

• Das Ergebnis ist der Flächeninhalt A des Dreiecks.
  

• Wenn g und h in cm waren, ist A in cm².
  

• Siehe auch Dreiecksfläche ↗
  

Sonstige Möglichkeiten

• Man hat ein rechtwinkliges Dreieck Rechtwinkliges Dreieck Fläche ↗
  

• Man kennt die Längen der drei Seiten Dreiecksfläche SSS ↗
  

• Mehr Sonderformeln unter Dreiecksflächenformeln ↗
  

Aufgaben