ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
1: Krümmung

Graphen

Gibt an, ob ein Funktionsgraph von links nach rechts gehend eine Links- oder Rechtskurve macht. Die Stärke der Krümmung spielt keine Rolle, nur die Richtung. Die Berechnung erfolgt über die zweite Ableitung f''(x). => Ganzen Artikel lesen …
2: Erdkrümmung

Geodäsie

Als Erdkrümmung bezeichnet man die Abweichung der Lage der wirklichen Erdoberfläche von einer perfekt geraden Ebene. Dass die Erde keine flache Scheibe ist, sondern möglicherweise eine Kugel geht mindestens bis zur Zeit von Pythagoras zurück [1]. Die Idee einer gekrümmten Ebene kann zu einer Kugelform passen, aber auch zu anderen Formen. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
3: Krängung

Gewollte Schräglage

Krängung bezeichnet die Neigung von Wasserfahrzeugen zur Seite, also eine Drehung um die Längsachse. => Ganzen Artikel lesen …
4: Brechung

Physik

Trifft ein Strahl [2], eine Welle [4] oder ein Teilchenstrom (z. B. Photonen) an eine Grenze zwischen zwei durchsichtigen Medien (z. B. Luft in Glas oder Luft in Wasser) oder ändert sich die Geschwindigkeit der Welle in einem Medium, dann kann es zu einer Änderung der Richtung kommen. Diesen Effekt nennt man in der Physik Brechung oder auch Refraktion [3]. Siehe mehr zu diesem Effekt unter => Brechung (Physik)
5: Raumkrümmung

Physik

Die Raumkrümmung ist ein Maß dafür wie stark ein Raum gekrümmt ist. Anschaulich kann man sagen: wie stark die geometrischen Gesetze dort von den uns bekannten euklidischen Gesetzen abweichen würden. Lies mehr dazu unter => gekrümmter Raum
6: Linkskrümmung

Definition

Bei einer Funktion f(x) spricht man dort von einer Linkskrümmung, wo ihr Graph zu einer nach oben geöffneten Schüssel, einem Smiley oder einer nach oben geöffneten Parabel ergänzt werden könnte. Das ist hier näher erklärt. => Ganzen Artikel lesen …
7: Ableitungsmethode für Krümmung

… siehe unter => Krümmung berechnen
8: Flächenkrümmung

Physik

Wie stark eine Fläche an einem bestimmten Punkt gekrümmt ist: der österreichische Physik-Professor Franz Exner definierte das Krümmungsmaß einer Fläche (z. B. ein Stück von einem Globus) über den Kehrwert zweier aufeineinander senkrecht stehender Krümmungsradien [1]. Ontologisch interessant ist die Extrapolation einer gekrümmten Fläche hin zu einem gekrümmte Raum. Lies dazu mehr im Artikel => gekrümmte Fläche
9: Flächenkrümmung und Winkelsummen

Physik

Dass die Summe der Innenwinkel in einem Dreieck immer exakt 180° gilt nicht immer. Bereits der Mathematiker Gauß zweifelte die Gültigkeit an. Gründe für diesen Zweifel und Konsequenzen für unser Weltbild sind hier erklärt. => Ganzen Artikel lesen …
10: Geometrische Krümmung

… siehe unter => Krümmungsmaß
11: Geradenkrümmung

Immer 0

Eine Gerade hat überall die Krümmung 0. Das heißt, sie ist an keiner Stelle links- oder rechtsgekrümmt. Das heißt analytisch, dass die zweite Ableitung f''(x) immer 0 ergibt, man sagt auch die zweite Ableitung verschwindet. Beispiel f(x) = 4x+8 ⭢ f'(x) = 4 ⭢ f''(x) = 0. Siehe auch => Parabelkrümmung [ähnlich]
12: Graph Krümmung

… siehe unter => Krümmung aus Graph
13: Graph mit Linkskrümmung

… zweite Ableitung größer als 0, mehr unter => Linkskrümmung
14: Graph mit Rechtskrümmung

… zweite Ableitung kleiner als 0, mehr unter => Rechtskrümmung
15: Graph und Krümmung

… siehe unter => Krümmung aus Graph
16: Graphenkrümmung ändert sich

… passt (vielleicht) auf einen => Wendepunkt
17: Graphenkrümmung bestimmen

… Verfahren für Funktionsgraphen unter => Krümmung bestimmen
18: Keine eindeutige Krümmung

… f''(x)=0 ist bezüglich der Krümmung mehrdeutig => zweite Ableitung gleich Null
19: Keine Krümmung

Übersicht

Graphen von Funktionen f(x) haben dort keine Krümmung, wo ihre zweite Ableitung f''(x) den Wert 0 annimmt. Ein geometrischer Raum oder eine geometrische Ebene gilt als nicht gekrümmt, wenn sie flach sind. Beides ist hier kurz erklärt. => Ganzen Artikel lesen …
20: Krümmung Ableitung

… siehe unter => Krümmung berechnen
21: Krümmung ablesen

… siehe unter => Krümmung aus Graph
22: Krümmung ablesen aus Graph

… siehe unter => Krümmung aus Graph
23: Krümmung ändert sich

… passt (vielleicht) auf einen => Wendepunkt
24: Krümmung Änderung

… passt (vielleicht) auf einen => Wendepunkt
25: Krümmung analytisch

… siehe unter => Krümmung berechnen
26: Krümmung anschaulich

… siehe unter => Krümmung aus Graph
27: Krümmung aus Ableitung

… siehe unter => Krümmung berechnen
28: Krümmung aus Funktionsgraph

… siehe unter => Krümmung aus Graph
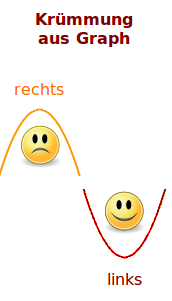29: Krümmung aus Graph

Aus einem Graphen ablesen, wie die Krümmung ist

Rechts-, links- oder gar nicht gekrümmt? Hier stehen einige Methoden, wie man die Art (nicht die Stärke) der Krümmung eines Graphen optisch ablesen kann. => Ganzen Artikel lesen …
30: Krümmung aus Graph ablesen

… siehe unter => Krümmung aus Graph
31: Krümmung aus zweiter Ableitung

… siehe unter => Krümmung berechnen
32: Krümmung ausrechnen

… Verfahren für Funktionsgraphen unter => Krümmung bestimmen
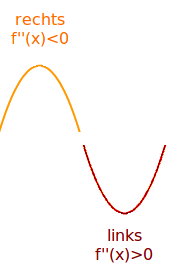33: Krümmung berechnen

f'' kleiner 0: rechtsgekrümmt; f'' größer 0: linksgekrümmt

f'' kleiner 0: rechtsgekrümmt; f'' größer 0: linksgekrümmt - das sind die wichtigsten Grundfakten zur rechnerischen Bestimmung der Richtung der Krümmung von einem Graphen. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
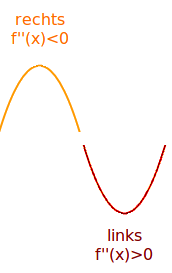34: Krümmung bestimmen

Mathematik

Von einer Krümmung spricht man sowohl bei Graphen der Mathematik, der Erdoberfläche oder auch bei Flächen und Räumen ganz allgemein. Auf dieser Seite hier wird kurz erklärt, wie man die Richtung der Krümmung eines mathematischen Graphen optisch und rechnerisch (über f'') bestimmt. Man weiß dann, wo der Graph links- und wo er rechtsgekrümmt ist. => Ganzen Artikel lesen …
35: Krümmung einer Parabel

… f(x)=4x² zum Beispiel links, mehr unter => Parabelkrümmung
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023