Flächen berechnen
Über Formeln
Das Wort Fläche wird oft für Flächeninhalt verwendet. Mit Flächeninhalt meint man, wie groß eine Fläche ist. Anschaulich wäre das, wie viel Farbe man bräuchte, um die Fläche einmal anzupinseln. Flächeninhalte kann man zum Beispiel in Quadratzentimetern oder Quadratmetern angeben. Mehr zur Definition unter => Fläche
Flächen
Verschiedene Arten (mathematisch)
Eine Fläche in der Mathematik (Geometrie) ist eine Teilmenge eines dreidimensionalen Raumes. Flächen werden üblicherweise als begrenzt (also nicht unendlich ausgedehnt) betrachtet. Sie können flach sein (Rechteckfläche) oder auch gekrümmt (Kugeloberfläche). Normalerweise werden sie als zusammenhängend betrachtet (verstreute Punkte bilden keine Fläche). Hier werden einige Arten kurz vorgestellt. => Ganzen Artikel lesen …
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
… Siehe unter => Flächenmaße umwandeln
Ein Hektar ist so viel wie 10 Tausend Quadratmeter und ein Quadratzentimeter sind 100 Quadratmillimeter. Anleitungen dazu unter => Flächenmaße umwandeln
Kugeln, Würfel, Quader, Pyramide etc.
Ein Würfel hat eine Oberfläche aber auch ein See oder ein Meer: Oberflächen können für 2D-Gewässeroberflächen oder für 3D-Körper berechnet werden. Beide Fälle werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Flächen bestimmen
Methoden
Rechnerisch oder auch anders: eine Fläche zu bestimmen heißt meistens, dass ihr Inhalt bestimmt werden soll: 40 cm², 5 Hektar oder 2850 m² wären typische Antworten. Liegt die Fläche in einer Ebene (2D, also zweidimensional) sagt man kurz auch Fläche. Die Außenfläche von Körpern hingegen nennt man meist eine Oberfläche (3D, dreidimensional). Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… Formeln unter => Kreisflächenformeln
A = ?
Flächen meint hier: zwischen Funktionsgraphen und der x-Achse. Wie das praktisch ausgeführt werden kann steht unter => Fläche unter der Kurve berechnen
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
Würfel, Quader, Prismen, Zylinder, Kegel
Die Mantelflächen sind anschaulich gesagt die senkrechten oder schräg nach oben gehenden Seitenflächen eines Körpers, wenn er auf der Grundfläche steht. Für verschiedene Körper gibt es angepasst Formeln, auf die hier verwiesen wird. => Ganzen Artikel lesen …
… siehe unter => Vieleckflächen berechnen
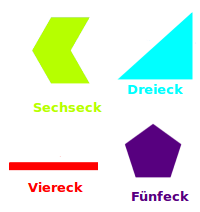
Dreiecke, Vierecke, Fünfecke etc.
Ein Vieleck ist eine flache 2D-Figur mit mindestens 3 Ecken. Zwischen den Ecken gibt es ausschließlich gerade Verbindungsstrecken. Typische Vielecke sind Dreiecke, Vierecke oder Achtecke. Zur Berechnung der Fläche unterscheidet man zwischen allgemeinen Vielecken und regelmäßigen Vielecken. Diese Fälle werden hier kurz vorgestellt. => Ganzen Artikel lesen …
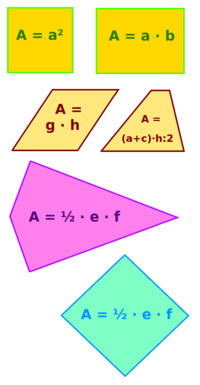
Vierecksflächen berechnen
Formeln
A in cm² oder m²: Quadrate, Rechtecke, Parallelogramme, Trapeze etc.: hier steht eine Übersicht zu verschiedenen Vierecksarten mit ihren jeweiligen Flächenformeln. => Ganzen Artikel lesen …
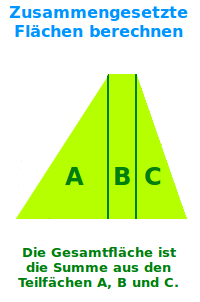
Zusammengesetzte Flächen berechnen
Anleitung
Oft kann man größere Flächen in mehrere kleine Flächen zerlegen. Für die so entstandenen Teilflächen gibt es oft spezielle Formeln mit denen sie (vergleichsweise) leicht berechnet werden können. Die Gesamtfläche ist dann gleich der Summe der Teilflächen. => Ganzen Artikel lesen …
