Zusammengesetzte Flächen berechnen
Anleitung
© 2016
- 2025
Basiswissen
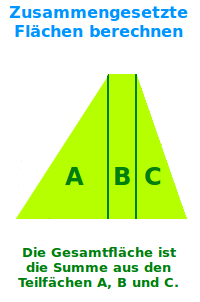
Oft kann man größere Flächen in mehrere kleine Flächen zerlegen. Für die so entstandenen Teilflächen gibt es oft spezielle Formeln mit denen sie (vergleichsweise) leicht berechnet werden können. Die Gesamtfläche ist dann gleich der Summe der Teilflächen.
Geometrie
Viele 2D-Figuren lassen sich leicht in mehrere sehr einfache Teilfächen zerlegen. Ein Trapez beispielsweise ist ein Viereck, bei dem mindestens zwei der vier Seitenlinien zueinander parallel sind. Jedes Trapez kann man in zwei Dreiecke und ein Rechteck zerlegen. Die Lösungsidee besteht immer daraus, Teilflächen zu finden, die man leicht berechnen kann. Man benutzt dazu fertige 👉 Flächenformeln
Integralrechnung
Die Integralrechnung beschäftigt sich mit Flächen in Koordinatensystemen. Dabei ist mindestens ein Rand durch den Graphen einer Funktion begrenzt. Durch Kombination verschiedener Geraden, Achsen und Graphen entstehen dabei oft Fragestellungen, bei denen zusammengesetzte Flächen die Lösungsidee geben. Für einen Einstieg, siehe unter 👉 Flächen über Integralrechnung
Ingenieurwesen
Für reale Bauteile (etwa die Flügeln einer Windraftanlage) müssen oft Spannungen oder Temperaturen für alle Stellen des Bauteils berechnet werden. Eine Methode dazu ist es, das Bauteil zuvor gedanklich in viele gegeineinander begrenzte (finite) Elemente zu zerlegen. Lies mehr unter 👉 Finite-Elemente-Methode