Anleitung
x = log von [y:a] zur Basis b - hier ist die Exponentialgleichung nach dem Exponenten, also der Hochzahl vom x umgestellt. Das ist mit Formel und Legende hier kurz vorgestellt. => Ganzen Artikel lesen …
Definition: die Unbekannte kommt im Exponenten vor
2 hoch 3x-9 = 64: eine Gleichung, bei der das x, das heißt die Unbekannte, im Exponenten steht heißt Exponentialgleichung [1]. Die Lösung im Beispiel ist x=5. => Ganzen Artikel lesen …
Lagewort
In dem Namen „Kasper“ steht der Buchstabe s nach dem Buchstaben a. Auch das p kommt erst nach dem a. Nach heißt so viel wie dahinter oder später. Eine Zahl, die direkt nach einer anderen Zahl kommt nennt man in der Mathematik einen => Nachfolger
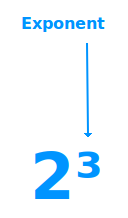Exponent
2ˣ⁺¹ und 4³
Ein Exponent ist ein Term oder auch eine einzelne Zahl, die in einer Potenz oben rechts, meist klein geschrieben steht. Bei 2ˣ⁺¹ ist das x+1 der Exponent. Bei 4³ ist die 3 der Exponent. => Ganzen Artikel lesen …
U=R·I wird zu I=U/R
Eine Formel umzustellen heißt, dass nach dem Umstellen eine andere Größe (ein anderer Buchstabe) links alleine vor dem Gleichzeichen steht wie am Anfang. Lies mehr dazu unter => Formeln umstellen
a = f(x) : b^x
a = f(x) : b^x - hier ist Exponential nach ihrem Start- oder Anfangswert (x=0) umgestellt. Das ist mit Formel und Legende kurz vorgestellt. => Ganzen Artikel lesen …
… ist erklärt unter => Exponentialgleichung nach Exponent umstellen
Aufgabentypen
Man hat verschiedene Angaben, zum Beispiele Texte oder Punkte. Daraus soll eine Gleichung wie etwa y = a·b^x oder eine Funktionsgleichung wie zum Beispiel B(t) = a·q^t aufgestellt werden. => Ganzen Artikel lesen …
… siehe unter => erweitere Exponentialgleichung umstellen
