 Dreieckshöhe
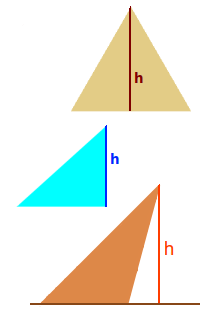
Dreieckshöhe
Definition
Jedes Dreieck hat drei Höhen: man wählt irgendeine der drei Dreiecksseiten aus und nennt sie g. Man wählt die Ecke gegenüber dieser ausgewählten Seite g. Man zieht eine Strecke von dieser Ecke so auf die ausgewählte Seite g, dass die Strecke mit der Seite g einen 90°-Winkel bildet. Das ist dann die Höhe über der Seite g. => Ganzen Artikel lesen …
 Dreieckshöhen
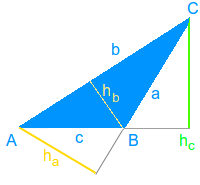
Dreieckshöhen
Definition
Jedes Dreieck hat drei Höhen: man stellt das Dreieck gedanklich auf eine beliebige seiner drei Seiten als Grundlinie. Dann gibt es genau eine obere Ecke. Die senkrechte Entfernung von der oberen Ecke zur Grundlinie ist dann die Höhe. => Ganzen Artikel lesen …
 Dreiecksfläche
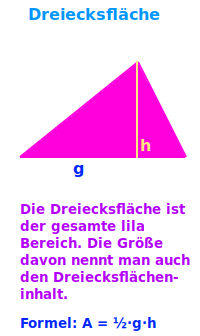
Dreiecksfläche
A=½·g·h
Die Dreiecksfläche ist die Fläche, die vom Rand des Dreiecks umschlossen wird. Will man die Größe dieser Fläche angeben kann man verschiedene Einheiten benutzen. Für sehr kleine Dreiecke eigenen sich mm² (Quadratmillimeter), für etwas größere nimmt man cm² (Quadratzentimeter, für große nimmt man m² (Quadratmeter) und für sehr große km² (Quadratkilometer). Eine übliche Abkürzung ist das große A. => Ganzen Artikel lesen …
Spezielles Ergebnis des Gauß-Algorithmus
Die Dreiecksform ist ein Sonderfall der Stufenform, bei der jede Zeile genau eine Unbekannte weniger als die vorhergehende hat. Das bedeutet, dass alle Koeffizienten der Hauptdiagonale von 0 verschieden sind. Die Dreiecksform entsteht bei Anwendung des gaußschen Eliminationsverfahrens, wenn das Gleichungssystem genau eine Lösung hat. => Ganzen Artikel lesen …
… siehe unter => Höhenlinien im Dreieck
… siehe unter => Dreieckshöhen
Rechenmethoden
Jedes Dreieck hat 3 Höhen. Sie können gleich lang aber auch verschieden lang sein. Zur Berechnung der Höhenlänge, z. B. in cm, gibt es verschiedene Verfahren. Welches man wählt hängt unter anderem davon, was von dem Dreieck gegeben ist. Hier werden einige Methoden kurz vorgestellt. => Ganzen Artikel lesen …
… etwa 0,5*a*1,73 mehr unter => Gleichseitiges Dreieck Höhe
… etwa 0,5*a*1,73 mehr unter => Gleichseitiges Dreieck Höhe
… also zeichnerisch, siehe unter => Dreieckshöhen konstruieren
Anleitung
Hier steht eine Schritt-für-Schritt Anleitung, wie man die Höhe in einem Dreieck konstruiert, also zeichnet. Ein Dreieck hat drei Höhen. Die Anleitung passt auf jede dieser drei Höhen. => Ganzen Artikel lesen …
… etwa 0,5*a*1,73 mehr unter => Gleichseitiges Dreieck Höhe
 Dreieckshöhenformeln
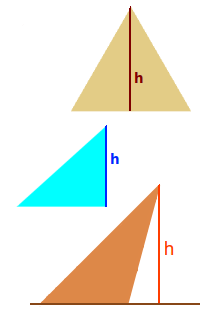
Dreieckshöhenformeln
Formeln zum Berechnen von Dreieckshöhen h
Je nachdem, was man von einem Dreieck kennt, kann man die Höhe h auf verschiedene Weisen ausrechnen. Hier werden einige Möglichkeiten vorgestellt. In den Zwischenüberschriften steht immer, was gegeben ist, darunter dann die passende Formel. => Ganzen Artikel lesen …
… etwa 0,5*a*1,73 mehr unter => Gleichseitiges Dreieck Höhe
… etwa 0,5*a*1,73 mehr unter => Gleichseitiges Dreieck Höhe
… Anleitung für Zirkelkonstruktion => Dreieckshöhen konstruieren
… Anleitung für Zirkelkonstruktion => Dreieckshöhen konstruieren
… Anleitung für Zirkelkonstruktion => Dreieckshöhen konstruieren
… Anleitung für Zirkelkonstruktion => Dreieckshöhen konstruieren
… Anleitung für Zirkelkonstruktion => Dreieckshöhen konstruieren

