Definition
≝ Genaue Beschreibung, was ein Wort meint
Laut Duden heißt definieren „den Inhalt [eines Begriffes] auseinanderlegen, erklären“ oder „bestimmen, festlegen; angeben oder beschreiben, worum es sich handelt“. Definieren ist lateinischen Ursprungs und heißt wörtlich: aus einer Grenze herleiten, begrenzen. Mit einer Definition legt man einen (möglichst) genauen Bedeutungsinhalt, auch Begriff genannt, für ein Wort oder Zeichen fest. => Ganzen Artikel lesen …
≝ Beispiele
Beispiele aus der Mathematik: Kreis, Kugel, Parallelogramm und so weiter. Was eine Definition ist, also eine Definition von Definition steht unter => Definition
Definieren
Wie ist definieren definiert?
Definieren heißt die Bedeutung eines Wortes möglichst eng und eindeutig festlegen. Beispiel: ein Planet ist ein Himmelskörper, der ein selbstleuchtendes Zentralgestirn umwandert und seine Umlaufbahn von anderen Körper leergeräumt hat. Lies mehr mehr zum Thema unter => Definition
Deflation
Dauerhaftes Sinken des Preisniveaus
Von einer Deflation spricht man, wenn sich die Preise für einen repräsentativen Warenkorb über längere Zeiträume hinweg verringern. Was zuerst gut klingt - alles wird billiger - hat allerdings auch unerwünschte Auswirkung: Erwartet man Preissenkungen für die Zukunft, dann hebt man Geld länger auf: es wird ja bald noch mehr wert sein. Dadurch wird weniger gekauft und die Wirtschaft gebremst. In Japan herrschte in den 1990er Jahren eine lange Deflation. Das Gegenteil einer Deflation ist eine => Inflation
≝ Beispiele
a⁰ ≝ 0 heißt: irgendeine natürliche Zahl hoch 0 gerechnet gibt per Definition immer als Ergebnis die Zahl eins. Es gibt keinen logisch zwingenden Grund, dass das so sein muss. Man hat es per Definition festgelegt. Siehe auch => Definition
… ist richtig geschrieben, umgangssprachlich auch => per Definition
… Annäherungen unter => Leben
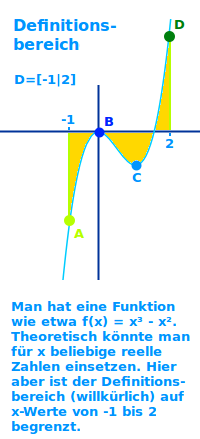Definitionsbereich
Definition
Alle Zahlen, zu denen es einen sinnvoll zuordenbaren y-Wert geben soll: das Wort Definitionsbereich wird zum Beispiel im Zusammenhang mit mathematischen Funktion, Aussagen oder Gesetzen gebraucht. Der Definitionsbereich sind alle x-Werte denen die Funktion eindeutig einen mathematisch oder sonstwie sinnvoll deutbaren y-Wert zuordnet. => Ganzen Artikel lesen …
… Abgrenzung unter => Definitionsbereich und Intervall
Erklärung im Sinne von Zuordnungen
Eine Funktion ordnet jedem Element einer Quellmenge (auch Definitionsbereich genannt) genau ein Element einer Zielmenge zu. Die Bildmenge besteht aus den Werten, die tatsächlich angenommen werden. => Ganzen Artikel lesen …
Abgrenzung und Gemeinsamkeiten
Der Definitionsbereich legt alle Zahlen fest, die man überhaupt in Betracht ziehen will oder erlaubt. Ein Intervall ist dann eine Auswahl davon, die man tatsächlich auch verwendet. Das wird hier näher erläutert. => Ganzen Artikel lesen …
Übersicht zu verschiedenen Begriffen
Die Begriffe gehören alle zu den Themen „Funktionen“ und „Gleichungen“. Die Worte unterscheiden einerseits die Zahlen, die man einsetzen darf (erlaubte x-Werte) und die rauskommen dürfen (mögliche y-Werte). Andererseits unterscheiden sie auch, was nicht nur rauskommen darf, sondern auch wirklich rauskommt (y-Werte die wirklich vorkommen). => Ganzen Artikel lesen …
Häufige aus der Schulmathematik
- => x Element der natürlichen Zahlen
Denkbare x-Werte einer Funktion, für die es keine y-Werte gibt
Eine Definitionslücke einer mathematischen Funktion ist ein x-Wert für den kein y-Wert angegeben ist. Der Definitionslücke gegenüber steht der Definitionsbereich: das sind alle x-Werte, für die auch ein y-Wert angegeben ist. Lies mehr dazu unter => Definitionslücken
Arten und Beispiele
Hebbare, Sprungstellen, Pol- und Oszillationsstellen: hier stehen einige Beispiele für mathematische Definitionslücken von Funktionen kurz erklärt. => Ganzen Artikel lesen …
… alle erlaubten x-Werte, heißt auch => Definitionsbereich
ist definiert als
Beispiel: x̄ = (a+b):2 => Ganzen Artikel lesen …
Definitionen
Ziffern rechts vom Komma nennt man Dezimale, ihre Position eine Dezimalstelle. Beides ist hier kurz auseinandergehalten. => Ganzen Artikel lesen …
Definintionen aus verschiedenen Quellen
Eine mathematische Definition sollte unter anderem dabei helfen, die folgenden Fragen mit ausschließlich ja oder nein beantworten zu können: => Ganzen Artikel lesen …
… alle Spalten sind gleich, Definition unter => Grenzmatrix
Definition
f(x) = x/sin(x) hat bei x=0 eine hebbare Definitionslücke bei x=0 und y=1: der Graph einer Funktion f(x) kann durch einen hinzugefügten Punkt wieder stetig gemacht werden, wo er vorher nicht stetig war. => Ganzen Artikel lesen …
Beispiele
Als hebbar bezeichnet man eine Definitionslücke einer Funktion f(x) bei der am Graph genau ein Punkt nicht definiert ist, der aber so ergänzt werden kann, dass der Graph anschließend stetig ist. Dazu stehen hier einige Beispiele. => Ganzen Artikel lesen …
… Abgrenzung unter => Definitionsbereich und Intervall
… Abgrenzung unter => Definitionsbereich und Intervall
… Abgrenzung unter => Definitionsbereich und Intervall
… Abgrenzung unter => Definitionsbereich und Intervall
… Bedeutung und Beispiele unter => nicht definiert
… Liste unter => Alogismen
… Liste mit unglücklichen Mathe-Worten => Alogismen
… Liste mit unglücklichen Mathe-Worten => Alogismen
… siehe unter => Singularität (Mathematik)
Gleichungen mit x^2
Das Dach ^ meint hoch zwei. Eine quadratische Gleichung, ist jede Gleichung, die man durch Umformungen in die folgende Form bringen kann: => Ganzen Artikel lesen …
… Liste unter => Alogismen
… Liste mit unglücklichen Mathe-Worten => Alogismen
… Von Geraden und Ebenen, siehe unter => Stützvektor
Der Begriff bezieht sich auf die Parameterform von 3D-Geraden. Jeder Vektor, der vom Koordinatenursprung (0|0|0) zu irgendeinem Punkt auf der Geraden führt, ist ein geeigneter => Stützvektor
