Bogenlänge über Integralrechnung
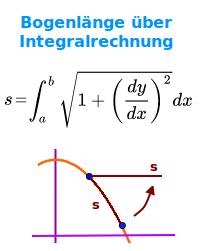
∫√[1+(f'(x))²]·dx
Auf einem Funktionsgraphen (Kurve) sind zwei Punkte gegeben. Die Bogenlänge s zwischen diesen Punkten ist definiert als der Abstand des gerade gestreckt gedachten Bogens. Die Länge kann mit Hilfe eines Integrals berechnet werden. => Ganzen Artikel lesen …
Bogenlänge
Mathematik
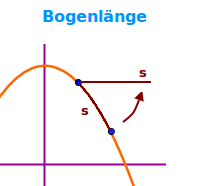
Die gestreckt gedachte Länge zwischen zwei Punkten entlang einer Linie nennt man die Bogenlänge. Ein Bogen im engeren Sinn ist eine gekrümmte Kurve. Im Zusammenhang mit Längenberechnungen schließt das Wort Bogenlänge aber die Berechnung gerader Teillängen meist mit ein. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Integralrechnung
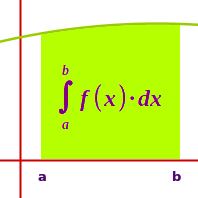
∫f(x)·dx
Zusammen mit der Differentialrechnung bildet die Integralrechnung das mathematische Teilgebiet der Analysis. Die Integralrechnung im engeren Sinn beschäftigt sich mit Flächenelementen von Graphen. In der Praxis spielt sie eine Rolle, wo die Effekte langfristig sich verändernder Prozesse aufsummiert werden. => Ganzen Artikel lesen …
A = ?
Über integrieren kann man viele Flächen recht einfach berechnen. Die dazu nötigen Methoden stehen unter => Fläche unter der Kurve berechnen
Analysis (Funktionsgraphen)
Mit Hilfe der Integralrechnung kann man unter anderem Flächeninhalte berechnen, bei denen einer oder mehrere Funktionsgraphen Ränder bilden. Es werden verschiedene Grundtypen entsprechender Aufgaben vorgestellt. => Ganzen Artikel lesen …
Beispiele
Viele Formeln lassen sich aus grundlegenden Tatsachen mit Hilfe der Integralrechnung herleiten. Entsprechende Beispiele sind unten zusammengestellt. => Ganzen Artikel lesen …
