F(b) - F(a)
Das bestimmte Integral von f(x)=6x soll berechnet werden in den Grenzen von 2 bis 4. Zuerst Stammfunktion bilden: F(x)=6x²/2 oder kurz: F(x)=3x². Dann rechnen: F(4)-F(2) = 48-12 = 36. Die Zahl 36 ist das Rechenergebnis für das bestimmte Integral. Der Rechenweg wird unten Schritt-für-Schritt erläutert. => Ganzen Artikel lesen …
∫: Definition
Das bestimmte Integral ist immer ein einzelner Zahlenwert. Ein unbestimmtes Integral hingegen ist eine Funktion. Neben dieser mathematischen Deutung heißt das Adjektiv integral auch so viel wie der wesentliche Teil von einem größeren Ganzen [1]. Hier wird die mathematische Bedeutung des Wortes Integral erklärt. => Ganzen Artikel lesen …
 Berechnen
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
 Bestimmtes Integral
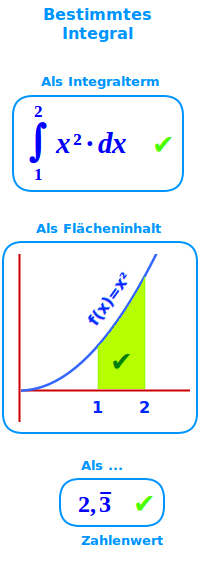
Bestimmtes Integral
Definition
Ein Integralterm mit angegebene Grenzen, auch der entsprechende Zahlenwert: das Wort Integral ist nicht sehr präzise. Es wird sowohl für eine Stammfunktion F(x) benutzt wie auch für Integralterme mit und ohne Angaben von Grenzen. Ein bestimmtes Integral hingegen ist immer ein Integralterm mit zwei als Zahlen angegebenen Grenzen. Ein solcher Term kann immer als Zahl ausgerechnet werden. Diese Zahl heißt oft auch bestimmtes Integral oder besser: Integralwert => Ganzen Artikel lesen …
… es gibt verschiedene, siehe zunächst unter => Integral
… siehe unter => Fläche unter der Kurve
Definition
Ein unbestimmtes Integral ist ein Integral bei dem eine oder beide der Integrationsgrenzen unbestimmt sind. Alternativ kann man auch sagen, dass die Integrationskonstante C unbestimmt ist. Alle drei Varianten einer Definition sind hier kurz vorgestellt. => Ganzen Artikel lesen …

