 Bahn
Bahn
Physikalisch
Flugbahnen, Fahrbahnen, Bahnen als mathematische Linie und Bahnen als Züge: verschiedene Bedeutungen sind hier kurz vorgestellt. => Ganzen Artikel lesen …
 Hahn
Hahn
… 🐓 ein männliches => Huhn
🦷 Definition
Ein Zahn ist ein Hartgebilde im Mundbereich von Wirbeltieren. Er besteht vor allem aus Kalziumphosphat. Das Wort ist indogermanischen Ursprungs und mit dem lateinischen dens verwandt. Lies mehr unter => Zähne
Bedeutungen
Ah als Amperestunden oder a·h als Term im Rahmen einer Flächenformel: hier werden verschiedene Bedeutungen kurz vorgestellt. => Ganzen Artikel lesen …
 U-Bahn
U-Bahn
… eine unterirdisch fahrende => Eisenbahn
 Achterbahn
Achterbahn
Schienengeführte Vergnügungsbahn
Achterbahnen erreichen Höhen von bis über 100 Metern (King da, New Jersey, 139 m) und Geschwindigkeiten bis 240 km/h (Formula Rossa, Abu Dhabi). => Ganzen Artikel lesen …
 Autobahn
Autobahn
… Eine breite Straße ausschließlich für Kraftfahrzeuge, siehe auch => Bahn
 Bahnberechnung
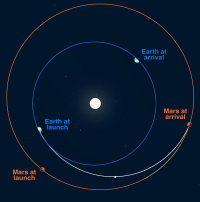
Bahnberechnung
Fachgebiete
Flugbahnen oder Umlaufbahnen: als Bahn oder Trajektorie bezeichnet man allgemein die Linie auf der sich ein loser Körper, seltener auch ein fest geführte Körper bewegt. Hier stehen Hinweise zu den Fachgebieten für eine Berechnung. => Ganzen Artikel lesen …
… entlang einer Kreislinie => Tangentialbeschleunigung
Astronomie
Eine Bahn in der Astronomie ist eine Linie, auf der sich ein Himmelskörper bewegt. Das können, müssen aber eine Kreise sein. In der Physik spricht man allgemein von einer => Trajektorie (Physik)
… Daten, wie der Erde um die Sonne wandert => Erdbahn
… Daten, wie der Venus um die Sonne wandert => Venusbahn
… Daten, wie der Jupiter um die Sonne wandert => Jupiterbahn
… Daten, wie der Mars um die Sonne wandert => Marsbahn
… Daten, wie der Merkur um die Sonne wandert => Merkurbahn
… Daten, wie der Neptun um die Sonne wandert => Neptunbahn
… Daten, wie der Uranus um die Sonne wandert => Uranusbahn
 Bahndrehimpuls
Bahndrehimpuls
Formelzeichen: L
Von einem Bahndrehimpuls spricht man, wenn eine Masse sich auf einer Kreisbahn um einen Mittelpunkt bewegt. Der Bahndrehimpuls steht anschaulich für den Schwung, der in der Kreisbewegung enthalten ist. Ein typisches Beispiel ist die Bahndrehimpuls des Monds bei seinem Umlauf um die Erde. => Ganzen Artikel lesen …
 Bahndrehimpuls berechnen
Bahndrehimpuls berechnen
Formeln
L = m·r·v oder L = m·r²·ω: der Bahndrehimpuls steht für die Wucht oder den Schwung der in der Bewegung einer Masse auf einer Kreisbahn enthalten ist. Ein klassisches Beispiel wäre der Bahndrehimpuls des Mondes auf seinem Weg um die Erde. => Ganzen Artikel lesen …
L = J·ω | L = m·v·r | L = m·ω·r²
Der Bahndrehimpuls L hat die Einheiten kg·m²/s oder N·m·s oder J·s. Die Größe steht anschaulich für die Wucht oder den Schwung der in einer Kreisbahnbewegung enthalten ist. => Ganzen Artikel lesen …
l
In der modellhaften Vorstellung von Elektronen in Bahnen um den Atomkern kann jedes Elektron einen Bahndrehimpuls haben. Ein Bahndrehimpuls ist anschaulich so etwas wie die Wucht, die in einer Kreisbahnbewegung enthalten ist. Die Bahndrehimpulsquantenzahl l - ein kleines lateinisches l - ist dasselbe wie die Orbitalquantenzahl l oder auch die => Nebenquantenzahl
Astronomie
Die Ebene, in der die Bahn eines Himmelskörpers liegt: von einer Bahnebene spricht man in der Astronomie und verwandten Gebieten. Himmelskörper bewegen sich oft auf Bahnen um einen anderen Himmelskörper, etwa die Erde um die Sonne. Stellt man sich ein flaches Blatt Papier gedanklich so vor, dass die Bahn ganz in dem Papier verläuft, dann ist das Papier die Bahnebene, beziehungsweise ein Teil davon. Die mathematische Ebene wird als unendlich weit ausgedehnt in alle Richtungen gedacht. Siehe mehr zur Definition im Artikel => Ebene
… in der Physik dasselbe wie die => Umlauffrequenz
 Bahngeschwindigkeit
Bahngeschwindigkeit
Physik
Als Bahn, Bahnkurve oder Trajektorie bezeichnet man die Linien - gerade oder gebogen - auf der sich ein Gegenstand bewegt. Die Bahngeschwindigkeit gibt an, wie schnell ein Gegenstand sich auf seiner Bahn bewegt. Übliche Einheiten sind zum Beispiel km/h oder m/s. Etwas anderes ist die Winkelgeschwindigkeit. => Ganzen Artikel lesen …
.png) Bahngeschwindigkeit (Astronomie)
Bahngeschwindigkeit (Astronomie)
Definition
Wenn sich ein Himmelskörper auf einer Umlaufbahn (Orbit) kann man ihm eine jeweils momentan gültige Bahngeschwindigkeit zuordnen. Die Bahnform kann elliptisch oder kreisförmig sein. Nicht-kreisförmige Bahnen sind behandelt unter dem Stichwort Zweikörperproblem. Hier werden nur kreisförmige Bahnen betrachtet. Die Bahngeschwindigkeit ist dann die Geschwindigkeit eines Körpers auf der Kreisbahn, zum Beispiel in m/s oder km/h oder oft km/s angegeben. => Ganzen Artikel lesen …
 Bahngeschwindigkeiten
Bahngeschwindigkeiten
Arten | Zahlenwerte
Als Bahngeschwindigkeit bezeichnet man eine Geschwindigkeit auf einer bestimmten Bahn, etwa einer Kreisbahn oder einer elliptischen Bahn. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
.png) Bahngeschwindigkeiten (Astronomie)
Bahngeschwindigkeiten (Astronomie)
Zahlenbeispiele
Die Bahngeschwindigkeit in der Astronomie gibt an, welche Strecke ein Objekt in einer bestimmten Zeit auf einer elliptischen oder kreisförmigen Umlaufbahn zurücklegt. => Ganzen Artikel lesen …
 Bahngewinnoptimierung
Bahngewinnoptimierung
Spieldaten für eine Optimierung mit zwei Variablen
Eine komplexe Aufgabenstellung, geeignet für verschiedene Lösungstrategien. => Ganzen Artikel lesen …
🚉 Definition
Ein Bahnhof ist ein Ort zum Umschlag von Gütern oder Menschen von Eisenbahnen auf andere Verkehrsmittel. Typisch sind Bahnsteige, Verkaufsschalter oder Automaten für Fahrkarten, Wartemöglichkeiten oder auch Lagerplätze für Transportgüter. Siehe auch => Loks
Physik
Als Bahnkurve allgemein bezeichnet man eine zusammenhängende Kurve, das heißt eine Linie, die durch jene Raumpunkte gebildet wird, die ein Massenpunkt durchläuft. [1] Das klassische Beispiele sind als Massepunkte idealisierte Himmelskörper oder Geschosse in der Ballistik. Spricht man von submikroskopisch kleinen Teilchen, etwa Elektronen in einer Nebelkammer, ist auch die Bezeichnung Teilchenbahn [2] üblich. Der Bahnbegriff macht Sinn in der klassischen Physik, nicht aber in der Quantenphysik, wo er keine Bedeutung hat. [1][2][3] Kurz Bahn oder auch Trajektorie sind Überbegriffe. Siehe mehr unter => Trajektorie (Physik)
 Bahnneigung
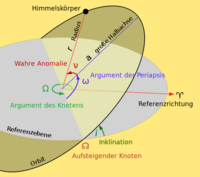
Bahnneigung
Astronomie
Als Bahnneigung bezeichnet man den Winkel zwischen der Bahnebene eines Himmelskörpers und einer zweiten Referenzebene. Für Satelliten in einem Erdorbit wählt man als Referenzebene meist die Äquatorebene der Erde. Für das Sonnensystem wählt man als Referenzebene meist die Ebene, in der die Erde um die Sonne läuft. Gegenüber dieser Ebene ist die Mondbahn zum Beispiel um etwa 5,2° geneigt. Die Berechnung von Bahnebenen ist Gegenstand der sogenannten => Himmelsmechanik
 Bahnradius
Bahnradius
r
Von einem Bahnradius r spricht man bei einer Kreisbewegung. So bewegt sich etwas der Mond in etwa auf einer Kreislinie um die Erde. Der Abstand des Mondmittelpunktes zum Erdmittelpunkt wäre dann ein Bahnradius. Der Bahnradius spielt eine wichtige Rolle bei vielen Berechnungen zur => Kreisbewegung
 Bahnumfang
Bahnumfang
Astronomie
Planeten oder andere Körper bewegen sich oft auf Kreis- oder Ellipsenbahnen um einen anderen Körper, den sogenannten Zentralkörper. Der Bahnumfang ist dann die Linie die einmal ganz um den Zentralkörper herumführt. Damit ist der Bahnumfang ein Sonderfall einer Umfangslinie. Siehe als Beispiel die => Mondbahn

=> Ganzen Artikel lesen …
 Berg- und Talbahn
Berg- und Talbahn
Physikalisch
Wagen fahren auf einer wellenförmig auf und ab gehenden Kreisbahn: dies Art von Fahrgeschäft gibt es seit etwa 1890. Die Insassen werden von dem Wagen nach innen gedrückt (Zentripetalkraft) und empfinden selbst eine nach außen schleudernde Fliehkraft (Zentrifugalkraft). Mit diesem Fahrgeschäft kann man sehr gut Geschwindigkeit und Kraft am eigenen Leib erfahren. => Ganzen Artikel lesen …

