Aussage
Logik
Ein Satz der wahr oder falsch sein kann: ein Pinguin ist immer auch ein Vogel. Ganz egal, ob diese Satz stimmt oder nicht: er kann entweder wahr oder falsch sein. Damit ist er aus logisch-mathematischer Sich eine Aussage [1][2], auch wenn der Wahrheitsgehalt selbst noch nicht geprüft wurde [5]. => Ganzen Artikel lesen …
Auslage
Übersicht
Im Schaufenster und als vorgestrecktes Geld: das Wort Auslage hat zwei Bedeutungen, die hier kurz vorgestellt sind. => Ganzen Artikel lesen …
Beispiele
3=4 ist eine typische mathematische Aussage, wennauch eine falsche. Ein nicht-mathematische Aussage (ebenfalls falsch) wäre: Der Mond ist größer als die die Erde. Hier stehen weitere Beispiele. => Ganzen Artikel lesen …
Ausgabe
… Die Verminderung des Geldvermögens einer Privatperson oder eines Unternehmens => Geldvermögen
Allaussage
Logik
Alle Vögel haben rote Schnäbel: ein Satz über alle Elemente einer Menge, der entweder wahr oder falsch sein kann. Es ist dabei unerheblich, ob er wahr oder falsch ist. Die Allaussage hier ist übrigens falsch. Keinen roten Schnabel hat zum Beispiel der Graupapagei => Ganzen Artikel lesen …
Eine Gleichung mit Unbekannten
Eine Aussage ist definiert als ein Satz, der entweder wahr ist oder falsch. „Wale sind Fische“ ist eine Aussage (wennauch eine falsche). Auch eine Gleichung ist eine Aussage: 3+4=7 ist eine wahr Aussage. Für eine Gleichung mit einer Unbekannten kann man aber noch nicht einmal theoretisch entscheiden, ob sie wahr ist oder nicht: x+3=10 ist für manche Werte von x falsch für den x-Wert 7 aber wahr. Solche Gleichungen mit Unekannten nennt man deshalb eine Aussageform. Setzt man für das x dann eine konkrete zahl ein, wird daraus eine => Aussage
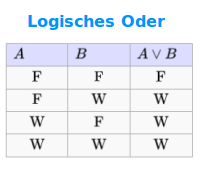Aussagenlogik
Mathematik
Die Aussagenlogik fragt, ob Schlüsse von gegebenen Prämissen (Ausgangsbehauptungen) korrekt gezogen wurden oder nicht. Die Aussagenlogik trifft keine Entscheidung darüber, ob die Ausgangsbehauptungen wahr sind oder nicht. => Ganzen Artikel lesen …
… in der Aussagenlogik die => Implikation
… in der Aussagenlogik die => Implikation
Das gegebene Pärchen bei Dreisatzaufgaben
Normale Dreisatz-Aufgaben bestehen immer aus zwei Pärchen. Bei einem sind beide Werte gegeben. Das ist der Aussagesastz. Beim anderen Pärchen fehlt eine der zwei Werte. Das gibt den Fragesatz. => Ganzen Artikel lesen …
Existenzaussage
Es gibt Ameisen mit rotem Körper
Eine Existenzaussage bezieht sich nur auf einen möglichen Einzelfall, auf einzelne Elemente einer größeren Menge. Es gibt Ameisen mit rotem Körper ist ein Beispiel. Eine Existenzaussage gilt als bewiesen, wenn man ein zutreffendes Beispiel gefunden hat. Sie ist damit deutlich schwäche als die umfassendere => Allaussage
Definition
Als falsch gilt eine Aussage, wenn sie nicht auf die Wirklichkeit zutrifft (der Mond ist ein Würfel) oder wenn sie Widersprüche mit als wahr anerkannten Aussagen erzeugt oder wenn. Ob eine Aussage wahr oder falsch ist entscheidet man mit sogenannten => Wahrheitskriterium
… in der Aussagenlogik, siehe unter => Logisches Nicht
… aus A folgt B und umgekehrt, siehe unter => logische Äquivalenz
Hartmut Bachmanns CO2-Aussage
Pseudowissenschaft
Ein Ausschnitt aus einem Vortrag des Publizisten Hartmut Bachmann (geboren 1924) aus dem Jahr 2009 wird hier als ein klassisches Beispiel für Pseudowisssenschaft vorgestellt. Hartmann hat durch eine sinnenverändernde Auslassung den fälschlichen Eindruck erweckt, dass der menschgemachte CO₂-Ausstoß nicht wesentlich zur gegenwärtigen Erderwärmung beiträgt. Durch Verwendung des Wortes „Klimalüge“ [1] unterstellte er Klimatologen eine vorsätzliche Irreführung bis hin zum Betrug [2]. Hartmanns pseudowissenschaftliche Argumentation ist hier im Detail beispielhaft vorgestellt. => Ganzen Artikel lesen …
Logik
3+1=4 und dass die Erde nahezu kugelförmig ist sind beides wahre Aussagen. 0°=1 und die Aussage, die Erde sei ein Würfel sind beide falsch. Um zwischen wahr und falsch unterscheiden zu können nutzt man verschiedene => Wahrheitskriterium
… in der Aussagenlogik die => Implikation
